Содержание
Пример 48.
В6.В магазине стоят два платежных автомата. Каждый из них может быть неисправен с вероятностью 0,05 независимо от другого автомата. Найдите вероятность того, что хотя бы один автомат исправен.
Решение:
Пусть А – «хотя бы один автомат исправен», 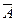 – «оба автомата неисправны».
Используя формулу умножения вероятностей независимых событий, получим:
Р( – «оба автомата неисправны».
Используя формулу умножения вероятностей независимых событий, получим:
Р(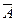 ) = 0,05∙0,05 = 0,0025.
Значит, вероятность того, что хотя бы один автомат исправен, по формуле вероятности противоположного события равна: Р(А) = 1 – Р( ) = 0,05∙0,05 = 0,0025.
Значит, вероятность того, что хотя бы один автомат исправен, по формуле вероятности противоположного события равна: Р(А) = 1 – Р(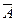 ) = 1 – 0,0025 = 0,9975.
В бланк ответов: 0,9975 ) = 1 – 0,0025 = 0,9975.
В бланк ответов: 0,9975
|
Пример 49.
В6. Два стрелка независимо друг от друга по одному разу стреляют в мишень. Вероятность попадания в мишень каждого стрелка в отдельности равна 0,8 и 0,6 соответственно. Найти вероятность того, что мишень не будет поражена ни разу.
Решение:
Пусть А – «первый стрелок попал в мишень», В – «второй стрелок попал в мишень». По условию Р(А) = 0,8, Р(В) =0,6, а А и В независимы. Вероятность того, что мишень не будет поражена ни разу, равна: 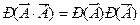 = (1-0,8)(1-0,6)=0,2 ∙ 0,4 = 0,08,
т.к. одновременно произошли события = (1-0,8)(1-0,6)=0,2 ∙ 0,4 = 0,08,
т.к. одновременно произошли события 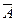 и и 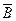 , т.е. произошло событие , т.е. произошло событие 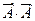 .
В бланк ответов: 0,08 .
В бланк ответов: 0,08
|
Пример 50.
| В6. Вероятность попадания в мишень при одном выстреле равна 0,8. Было произведено 3 независимых друг от друга выстрела. Найти вероятность того, что мишень будет поражена трижды. Решение: Пусть А – «мишень поражена при первом выстреле», В – «мишень поражена при втором выстреле», С - «мишень поражена при третьем выстреле». По условию Р(А) = Р(В) = Р(С) = 0,8. События А, В, С попарно независимы. Вероятность того, что мишень будет поражена трижды, равна: Р(А·В·С)=Р(А)Р(В)Р(С)= 0,8³ = 0,512, т.к. одновременно произошли события А, В и С, т.е. произошло событие А·В·С. В бланк ответов: 0,512 |
Пример 51.
В6. Вероятность попадания в мишень при одном выстреле равна 0,7. Было произведено 3 независимых друг от друга выстрела. Найти вероятность того, что мишень не будет поражена.
Решение:
Пусть А – «мишень поражена при первом выстреле», В – «мишень поражена при втором выстреле», С - «мишень поражена при третьем выстреле». Тогда 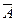 - промах. По условию Р(А) = 0,7, значит, Р( - промах. По условию Р(А) = 0,7, значит, Р( 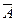 ) =1 – 0,7 = 0,3. События А,В, С попарно независимы.
Вероятность того, что мишень не будет поражена, равна: ) =1 – 0,7 = 0,3. События А,В, С попарно независимы.
Вероятность того, что мишень не будет поражена, равна:
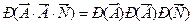 = (1-0,7)³=0,3³ = 0,027,
т.к. одновременно произошли события = (1-0,7)³=0,3³ = 0,027,
т.к. одновременно произошли события 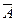 , , 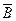 и и 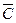 , т.е. произошло событие , т.е. произошло событие 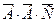 .
В бланк ответов: 0,027 .
В бланк ответов: 0,027
|
 2015-03-20
2015-03-20 654
654








