1. Задача Фламана решена для плоского напряженного состояния при условии отсутствия поперечной деформации (плоская деформация) и методологически подобна задаче Буссинеска для полупространства. По этой причине рассмотрим лишь конечные результаты решения этой задачи. Пусть на поверхности полупространства (рис. 4.1) действует бесконечно протяженная полосовая нагрузка q (кН/м) вдоль координатной оси x единичной ширины.
|
|
|
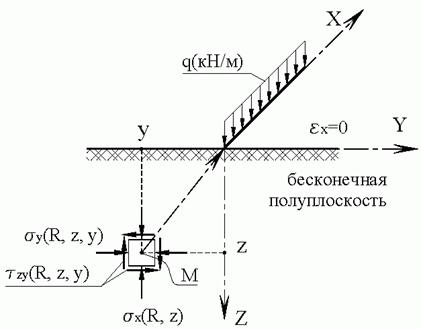
Тогда в сечениях полупространства плоскостями, нормальными к оси x, будем иметь полуплоскости, напряженно-деформированное состояние которых подобно, а деформация по направлению оси x равна нулю. Как уже отмечалось, такое напряженное состояние называется плоской деформацией. Напряжения в точке М полуплоскости с радиусом-вектором R и координатами y, z в соответствии с решением Фламана определяются формулами:
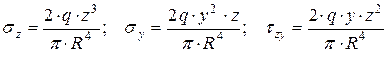 . (4.1)
. (4.1)
Практический интерес представляет распределение напряжений в полуплоскости от действия бесконечно протяженной полосовой нагрузки (рис. 4.2) конечной ширины В. Подобное напряженное состояние возникает в поперечных сечениях основания протяженного ленточного фундамента.
|
|
|
|
|
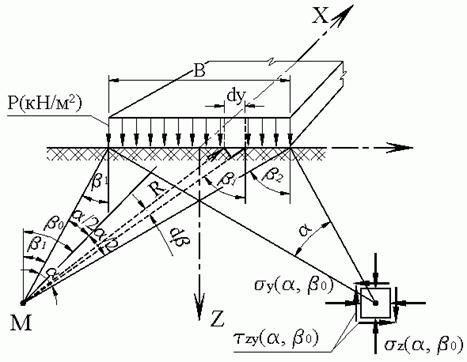
Пусть интенсивность нагрузки в пределах полосы постоянна и равна р (кН/м2). Соединим точку М с концами полосовой нагрузки в сечении полуплоскостью. Угол между проведенными таким образом лучами из точки М назовем углом видимости a. Интенсивность полосовой нагрузки dq шириной dy будет равна: dq = p × dy = p × R × db / cosbi, где bi – угол между вертикалью и лучом, проведенным из точки М к площадке dy; db – угол видимости площадки dy. Граничными значениями угла bi будут углы b1 и b2, составляемые с вертикалью лучами угла видимости a. Положительное направление указанных углов отсчитывается от вертикали при повороте ее в сторону луча по ходу часовой стрелки. Подставляя в уравнения (4.1) вместо q dq и производя их интегрирование по b, получим выражения для определения напряжений в грунтовом массиве от полосовой нагрузки:
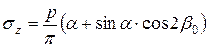
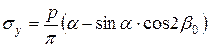
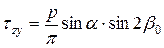
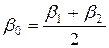 . (4.2)
. (4.2)
Можно показать, что b0 = b1 + a/2. При b0 = 0 b1 = - a /2, а b2 = a /2. Отсюда следует, что нормальные напряжения sz по оси симметрии полосовой нагрузки являются главными напряжениями, так как касательные напряжения tzy на площадках действия указанных напряжений равны нулю. Напряженному состоянию с компонентами тензора напряжений (4.2) соответствуют главные напряжения:
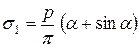 ;
;
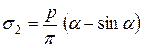 . (4.3)
. (4.3)
Угол наклона площадки большего главного напряжения к площадке напряжения sz будет равен:
|
|
|
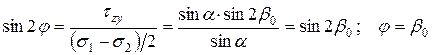 . (4.4)
. (4.4)
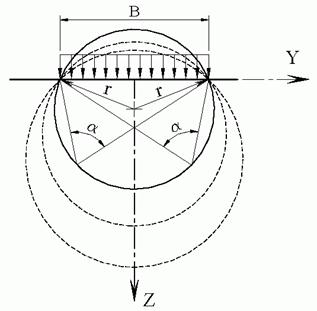
Из уравнения (4.4) следует, что нормалью к площадке больших главных напряжений является биссектриса угла видимости a. Говорят также, что большая главная ось эллипса напряжений в точке М совпадает по направлению с биссектрисой угла видимости в этой точке (рис. 4.3). Можно доказать (рис. 4.4), что геометрическим местом точек с одинаковыми значениями главных напряжений являются окружности, проведенные через крайние точки полосовой нагрузки.
|
|
2. Закономерности распределения напряжений. Изобары, распоры, сдвиги.
|
|
|
|
|
|
|
|
|
|
|
|
|
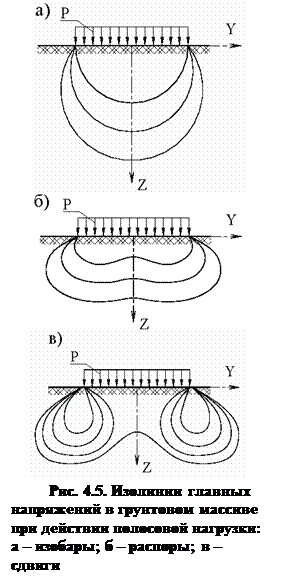 Изобарами называют линии равных вертикальных давлений (рис. 4.5 а). Распорами называют линии равных боковых давлений (рис. 4.5 б). Сдвигами называют линии равных касательных напряжений (рис. 4.5 в). Указанные линии строятся как графики sz = const, sy = const, tzy = const, например, с использованием уравнений (4.2). С удалением от центра загруженной поверхности и с увеличением глубины вертикальные давления уменьшаются. При этом линии равных давлений подобны концентрическим усеченным эллипсам с главной вертикальной осью, проходящей через центр загруженной поверхности. Горизонтальными сечениями изобар можно проследить закономерности изменения давлений по ширине грунтового массива. Общая закономерность сводится к следующему. С увеличением глубины интенсивность давлений уменьшается, а зона их действия по ширине увеличивается. При этом площади эпюр давлений в горизонтальных сечениях остаются постоянными. В несвязных грунтах можно приблизительно полагать, что область распределения давлений в грунтовом массиве ограничена расходящимися лучами, исходящими из крайних точек загруженной поверхности и наклоненными к горизонтали под острыми углами, равными углу внутреннего трения.
Изобарами называют линии равных вертикальных давлений (рис. 4.5 а). Распорами называют линии равных боковых давлений (рис. 4.5 б). Сдвигами называют линии равных касательных напряжений (рис. 4.5 в). Указанные линии строятся как графики sz = const, sy = const, tzy = const, например, с использованием уравнений (4.2). С удалением от центра загруженной поверхности и с увеличением глубины вертикальные давления уменьшаются. При этом линии равных давлений подобны концентрическим усеченным эллипсам с главной вертикальной осью, проходящей через центр загруженной поверхности. Горизонтальными сечениями изобар можно проследить закономерности изменения давлений по ширине грунтового массива. Общая закономерность сводится к следующему. С увеличением глубины интенсивность давлений уменьшается, а зона их действия по ширине увеличивается. При этом площади эпюр давлений в горизонтальных сечениях остаются постоянными. В несвязных грунтах можно приблизительно полагать, что область распределения давлений в грунтовом массиве ограничена расходящимися лучами, исходящими из крайних точек загруженной поверхности и наклоненными к горизонтали под острыми углами, равными углу внутреннего трения. Распределение распоров характеризуется наличием седловидной впадины в центре загруженной поверхности. Максимальных значений распоры достигают на границах области распределения вертикальных давлений.
Сдвиги распределяются в форме двух симметричных зон с центрами по краям загруженной поверхности. Геометрически указанные распределения подобны концентрическим эллипсам, главные большие оси которых наклонены и расходятся от центра загруженной поверхности. Максимальные значения сдвигов достигаются (концентрируются) в крайних точках загруженной поверхности. Этот результат уже использовался при описании фаз напряженно-деформированного состояния грунтового основания.
3. Контактные напряжения. До сих пор изучались вопросы распределения напряжений от действия распределенной по площади нагрузки. Нагрузка передавалась непосредственно на поверхность грунтового массива без посредства какой-либо конструкции. Такая схема передачи нагрузки характерна при возведении на основании земляных сооружений, например, насыпей, при передаче нагрузки через гибкую плиту и т.п. Во всех этих случаях говорят, что нагрузка передается на основание через абсолютно гибкий штамп. Таким образом, абсолютно гибким штампом называют конструкцию, сопротивлением изгибу которой можно пренебречь. Нагрузка на основание от сооружений чаще всего передается через жесткие конструкции, называемые фундаментами. Если собственными деформациями такой конструкции можно пренебречь, ее называют абсолютно жестким штампом. Все остальные конструкции, через которые передается нагрузка на основание, называют фундаментами (говорят также, штампами конечной жесткости). Контактными напряжениями называют напряжения на контакте поверхности основания с нижней поверхностью конструкции, через которую передаются нагрузки. Нижняя поверхность такой конструкции называется подошвой фундамента. Вертикальные напряжения, действующие на основание со стороны подошвы фундамента, называют давлениями. Уравновешивающие эти давления напряжения, действующие на подошву фундамента со стороны основания, называют отпором грунта. Решим задачу о распределении давлений на основание под жестким штампом при действии на него вертикальной нагрузки.
|
|
|
Воспользуемся формулой, полученной Буссинеском, для определения осадок (вертикальных перемещений) wz поверхности линейно-деформируемого полупространства (рис. 4.6) от действия сосредоточенной силы Р:
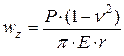 , (4.5)
, (4.5)
где n, Е – коэффициент Пуассона и модуль деформации грунта;
r – расстояние от точки приложения силы до точки, в которой вычисляется осадка (радиус-вектор).
|
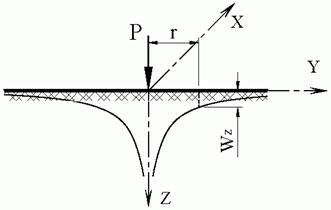
Используя формулу (4.5), определим осадку в точке с координатами x, y (рис. 4.7) от распределенной по площади F нагрузки интенсивностью р (кН/м2). При этом учтем, что элементарная сосредоточенная сила dP = p×dx × dh, а радиус-вектор r = [(x - x)2 + (y - h)2]1/2.
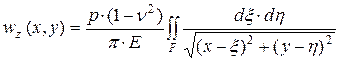 . (4.6)
. (4.6)
Исследованиями по теории упругости установлено, что осадка абсолютно жесткого штампа с достаточной для практических целей точностью равна средней осадке абсолютно гибкого штампа. Средняя осадка абсолютно гибкого штампа может быть вычислена интегрированием по площади выражения (4.6) с последующим делением результата на площадь подошвы F:
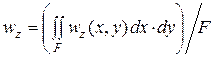 . (4.7)
. (4.7)
|
|
|
|
|

Рис. 4.7. Осадка поверхности упругого полупространства от действия распределенной по площади F нагрузки интенсивностью р (кН/м2)
Принимаем в выражении (4.6) wz (x, y) = wz = const и разрешая его относительно р как функции x, y, получим формулу для распределения давлений p (x, y) под абсолютно жестким штампом:
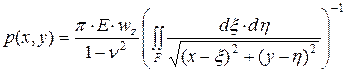 . (4.8)
. (4.8)
Наиболее простой вид решение уравнения (4.8) приобретает для штампа круглой формы в плане:
|
|
|
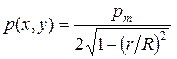 , (4.9)
, (4.9)
где pm – среднее давление под подошвой штампа; r –радиус-вектор точки, в которой вычисляется контактное давление p (x, y); R – радиус круглого штампа.
Аналогичное решение получено для плоской задачи (плоская деформация). Формула для вычисления контактных давлений под абсолютно жесткой бесконечной полосой имеет вид:
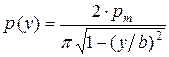 , (4.10)
, (4.10)
где y – координата точки, в которой определяется давление p (y); b – половина ширины полосы.
В помещаемой ниже таблице приведены сопоставительные данные о распределении контактных давлений под штампами разной конструкции при одинаковом значении среднего давления.
Таблица 4.1
| Конструкция штампа | Абсолютно жесткий круглый диаметром R | Абсолютно жесткая полоса шириной 2× b | Абсолютно гибкая полоса шириной 2× b |
| Давление в центре | pm / 2 | 2×pm / p | pm |
| Давления по краям | ¥ | ¥ | pm |
Как следует из таблицы, давления в центре жестких штампов меньше средних давлений. При удалении от центра контактные давления возрастают и стремятся к бесконечности в краевых точках. Давления в центре и по краям гибкого штампа равны заданному давлению на загруженной поверхности. Таким образом, конструкция штампа существенно влияет на характер распределения контактных давлений. Данные таблицы 4.1 интерпретированы графически на рис. 4.8. На этом же рисунке представлены графики распределения контактных давлений под штампами конечной жесткости. Анализируя эти графики, можно сделать следующий вывод: контактные давления под штампами конечной жесткости находятся в диапазоне соответствующих давлений для абсолютно жесткого и абсолютно гибкого штампов. Следует также обратить внимание на то, что в реальных грунтах контактные давления не могут неограниченно возрастать, так как их значения ограничиваются параметрами прочности основания.
|
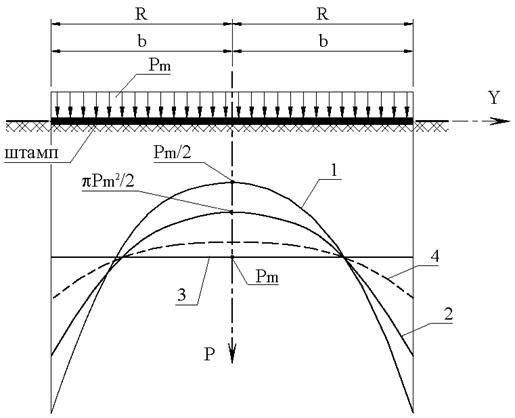
Рис. 4.8. Распределение контактных давлений по подошве: 1 – абсолютно жесткого круглого штампа; 2 – абсолютно жесткой полосы; 3 – абсолютно гибкой полосы;
4 – штампа конечной жесткости
На основании обобщения результатов теоретических и экспериментальных исследований фундаментов конечной жесткости на грунтовых основаниях в нормах на проектирование оснований принят линейный закон распределения контактных давлений по подошве фундаментов. Эта гипотеза равносильна гипотезе плоских сечений в теории строительных конструкций. В связи с этим контактные давления определяются по упрощенной формуле:
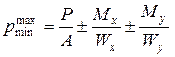 , (4.11)
, (4.11)
где P, Mx, My – продольная сила и изгибающие моменты относительно центральных осей на уровне подошвы фундамента;
A, Wx, Wy – площадь подошвы и моменты сопротивления площади подошвы фундамента относительно центральных осей.
4. Напряжения от собственного веса грунта. Вертикальные напряжения от собственного веса грунта называют бытовыми давлениями, а график их изменения по глубине – эпюрой бытовых давлений. Напряжения от собственного веса грунта определяются на основании следующих упрощающих гипотез: 1) напряженным состоянием грунта при действии его собственного веса является осесимметричное компрессионное сжатие; 2) вертикальные напряжения в грунте определяются суммированием напряжений от веса элементарных слоев грунта; 3) грунт, находящийся ниже уровня грунтовых вод, испытывает взвешивающее действие воды; 4) слой грунта, находящийся ниже водоносного слоя, называется водоупором и испытывает на своей поверхности гидростатическое давление водяного столба.
Удельный вес грунта во взвешенном состоянии определяется на основании следующих расчетов. Обозначим: Gsb (кН) – вес грунта объемом V (м3) во взвешенном состоянии; Gs, Vs – вес и объем частиц грунта в объеме V; gd, gs, и gw – удельные веса сухого грунта, частиц грунта и воды. Определим Gsb и gsb – удельный вес грунта во взвешенном состоянии:
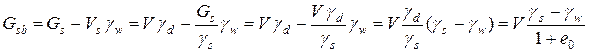
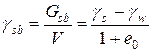 . (4.12)
. (4.12)
С учетом сделанных замечаний, бытовые давления в грунте определяются методом послойного суммирования:
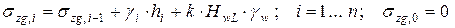 , (4.13)
, (4.13)
где gi – g или gsb для i –го слоя грунта; hi – толщина i –го слоя грунта;
HwL – расстояние от водоупора до уровня грунтовых вод; k – коэффициент, равный 1 для границы водоупора и 0 в остальных случаях.
Формула (4.13) используется для вычисления бытовых давлений на границах геологических слоев, на линии уровня грунтовых вод и на границе водоупора. В остальных сечениях бытовые давления могут быть определены по линейной интерполяции. На рис. 4.9 представлены характерные эпюры бытовых давлений в грунтовом массиве. На границах геологических слоев угол наклона эпюры, как правило, изменяется в связи с изменением величины удельного веса грунта. На линии уровня грунтовых вод (WL) имеет место самый заметный перегиб эпюры, вызванный уменьшением удельного веса грунта во взвешенном состоянии. На границе водоупора эпюра имеет скачок на величину гидростатического давления от веса столба воды над водоупором.

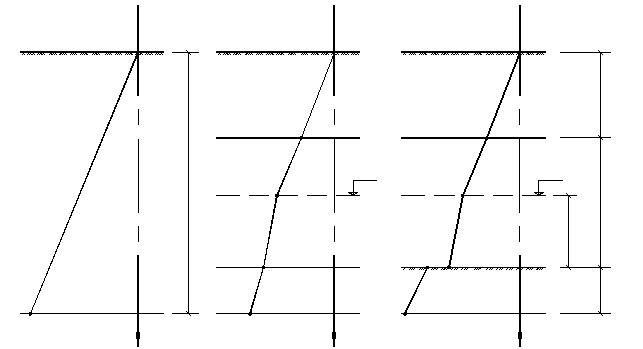
Рис. 4.9. Характерные эпюры распределения бытовых напряжений в массиве грунта: а) – однородный массив; б) – массив, представленный тремя инженерно-геологическими элементами; в) – то же, но при этом третий слой является водоупором
Лекция 5. Теория предельного напряженного состояния грунта. Задача Пузыревского. Начальные и предельные критические давления. Огибающие зон предельного равновесия. Давление грунта на подпорные стены. Устойчивость подпорных стен
Предельное напряженное состояние грунта принято анализировать методами предельного равновесия. В современной механике грунтов применяются также методы, основанные на решении смешанной задачи теории упругости и теории пластичности, а также методы теории пластического течения. Уравнения метода предельного равновесия для условий плоской задачи имеют вид:
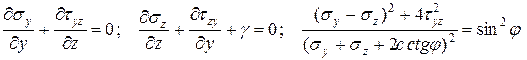 , (5.1)
, (5.1)
где sy, sz, tyz – компоненты тензора напряжений; g – удельный вес грунта;
c, j – параметры прочности грунта.
Решение системы уравнений (5.1) совместно с краевыми условиями позволяет установить зоны, в которых грунт находится в состоянии предельного равновесия.
1. Предельное напряженное состояние грунта под полосовой нагрузкой. Задача Пузыревского. Основными гипотезами, при которых решена задача Пузыревского, являются следующие: 1) компоненты напряжений распределяются в грунтовом массиве в соответствии с решением Фламана для плоской деформации; 2) коэффициент бокового давления грунта в предельном состоянии равен единице. Экспериментальными исследованиями установлено, что введенные гипотезы позволяют получать решения с точностью, достаточной для практики.
Пусть на поверхности грунтового массива (рис. 5.1) задана полосовая нагрузка интенсивностью p - g × h и бесконечно протяженная распределенная нагрузка интенсивностью g × h, так что в пределах полосы суммарная интенсивность нагрузки составляет р (кН/м2). Нагрузку g × h можно рассматривать как пригруз поверхности грунтового массива насыпью высотой h. Напряжения в грунтовом массиве будут складываться из напряжений от полосовой нагрузки интенсивностью p - g × h и напряжений от собственного веса грунта с учетом насыпи на его поверхности высотой h. Используя формулы для определения указанных напряжений, полученные ранее, будем иметь:
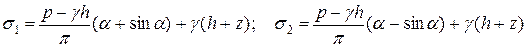 . (5.2)
. (5.2)
|
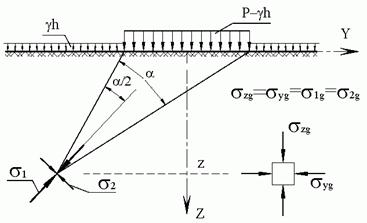
Полученные формулы являются решением системы дифференциальных уравнений равновесия (5.1) применительно к рассматриваемой задаче. Условие предельного равновесия примем в форме закона Кулона–Мора для главных напряжений:
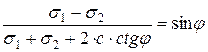 ; (5.3)
; (5.3)
Подставляя напряжения (5.2) в формулу (5.3), получим уравнение предельного равновесия весомого грунта под полосовой нагрузкой с учетом пригруза на поверхности:
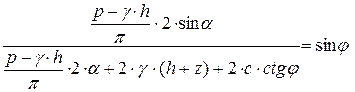 ;
;
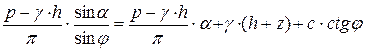 ;
;
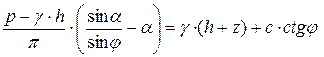 ;
;
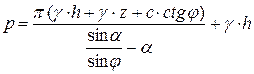 . (5.4)
. (5.4)
Полученное уравнение предельного равновесия устанавливает зависимость между интенсивностью полосовой нагрузки р и координатами точки предельного равновесия z и a. Варьируя значениями координат z и a, можно установить области пластического деформирования грунта при р = const. Такие решения справедливы для малых областей пластического деформирования и весьма приближенны для развитых пластических зон. Объясняется это тем, что в основе формулы (5.4) лежит решение о распределении напряжений в грунтовом массиве в упругой постановке. В действительности напряжения в пластических зонах не подчиняются законам упругости. Поэтому с развитием пластических зон уменьшается достоверность результатов решения задачи по формуле (5.4). Практический интерес представляет минимальное значение полосовой нагрузки при развитии зон пластического деформирования на глубину z. Этому значению нагрузки соответствует максимальное значение знаменателя в формуле (5.4). Значение координаты a, соответствующее максимальному значению знаменателя, определяется из уравнения:
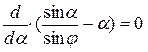 ;
; 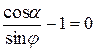 ;
;
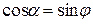 ;
; 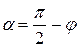 ;
; 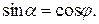 (5.5)
(5.5)
Подстановкой выражений (5.5) в формулу (5.4) получаем критическое значение полосовой нагрузки, соответствующее развитию зон пластического деформирования на глубину z:
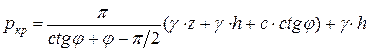 . (5.6)
. (5.6)
Начальным критическим давлением называют интенсивность нагрузки, которая соответствует началу образования зон пластического деформирования. Таким образом, начальное критическое давление при полосовой нагрузке может быть определено по формуле (5.6) при подстановке в нее нулевого значения координаты z:
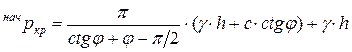 . (5.7)
. (5.7)
Выражение (5.7) является формулой Пузыревского, полученной им для равномерно распределенной нагрузки по полосе в условиях плоской деформации. Имеются аналогичные решения для других видов напряженного состояния и нагрузок, например, решение Прандтля для осесимметричной пространственной задачи при распределении нагрузки по кругу и т.п. Из формулы (5.7) следует, что грунтовое основание обладает несущей способностью даже в том случае, когда равны нулю прочностные характеристики грунта с и j. В этом случае его прочность обеспечивается пригрузом (слагаемое g × h). Использование пригруза для повышения прочности основания является основным методом строительства на слабых грунтах (илах, торфах). Как уже отмечалось, начальное критическое давление является границей между фазами уплотнения и сдвига. Поскольку в фазе уплотнения применим принцип линейной деформируемости, говорят также, что начальное критическое давление является пределом пропорциональности между давлениями и осадками (напряжениями и деформациями). В нормах строительного проектирования в качестве предела пропорциональности принимают величину, несколько превышающую начальное критическое давление, называемую расчетным сопротивлением грунта. Расчетное сопротивление грунта это критическое давление, при котором зоны пластического деформирования распространяются на глубину В /4, где В – ширина фундамента. Величину расчетного сопротивления грунта можно оценить с помощью формулы (5.6) при подстановке в нее вместо z à B /4.
2. Огибающие зон предельного равновесия. Предельное критическое давление. Выполним качественный анализ формирования зон предельного равновесия с помощью формулы (5.6). Траектория точек с одинаковыми значениями углов видимости изобразится в виде окружности, симметричной относительно полосовой нагрузки и проходящей через крайние точки этой нагрузки. Для угла видимости (p /2 - j), соответствующего минимальному значению нагрузки при распространении зон пластического деформирования на глубину z, графические построения представлены на рис. 5.2.
Зоны пластического деформирования зарождаются по краям нагрузки и с ее увеличением распространяются в глубину. Слияние зон пластического деформирования в одну большую зону под всей нагрузкой произойдет под центром нагрузки на глубине, где горизонталь z = const касается окружности. Можно предположить, что с этого момента осадка основания будет происходить без приращения нагрузки, а достигнутый уровень нагружения является предельным. Таким образом, предельное критическое давление это нагрузка, при которой зоны предельного равновесия сливаются в одну общую зону, отделяющую нагрузку от нижележащего массива грунта.
|
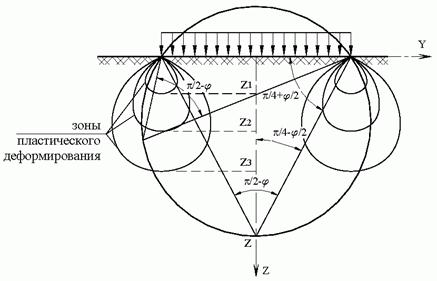
Как уже отмечалось, предельное критическое давление является границей между фазами сдвигов и выпора. Для сопоставления приведем значения начального и предельного критических давлений при полосовой нагрузке для идеально связного грунта (j = 0): начркр = p × с + g × h; предркр = (2 + p) + g × h. Последняя формула была получена Прандтлем на основании постулирования огибающей зон предельного равновесия в грунтовом массиве. В нормах на проектирование оснований принята форма огибающих зон предельного равновесия, предложенная Березанцевым (рис. 5.3, условно показана только левая часть симметричного графика). Решение сведено к трехчленному уравнению с протабулированными коэффициентами:
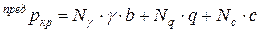 , (5.8)
, (5.8)
где Ng, Nq, Nc – коэффициенты, функционально зависящие от угла внутреннего трения j; с – сцепление; b – ширина фундамента; q = g × h – пригруз.
|
|
Как уже отмечалось, в современной механике критические давления на грунт чаще всего определяются из решения смешанной задачи теории упругости и теории пластичности с использованием алгоритмов, реализуемых на ПЭВМ. Достоинством таких решений является установление функциональных зависимостей осадок от давлений в фазах сдвигов и выпора грунта. Замкнутые аналитические решения, позволяющие получить такой результат, в нормах на проектирование оснований отсутствуют. По этой причине давления на основания ограничивают величиной расчетного сопротивления грунта, а осадки рассчитывают с использованием линейной теории.
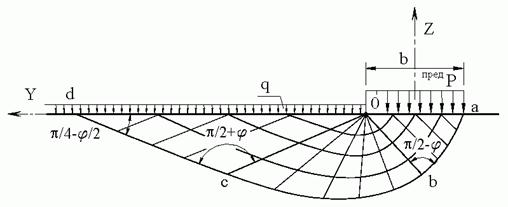
3. Давление грунта на подпорные стены. Подпорной стеной называют конструкцию, воспринимающую горизонтальные давления грунтового массива, находящегося в состоянии предельного равновесия. Рассмотрим подпорную стену с вертикальной и абсолютно гладкой поверхностью, обращенной в сторону грунтового массива (рис. 5.4).
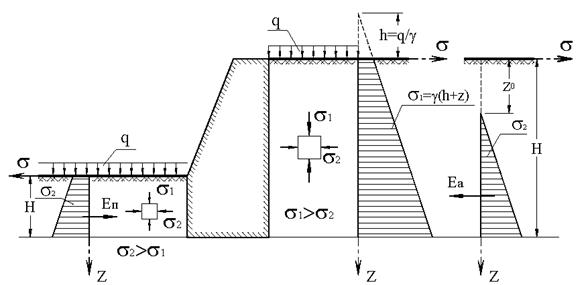
Рис. 5.4. Расчетная схема для определения величин активного и пассивного давления грунта на подпорную стену
Эти условия позволяют рассматривать давление грунта на боковую поверхность стены как главные напряжения s2, действующие в грунтовом массиве на вертикальных площадках. На горизонтальных площадках действуют напряжения s1 от собственного веса грунтового массива и от пригруза q (кН/м2) на его поверхности. Поверхность грунтового массива предполагается горизонтальной, а пригруз представляется весом насыпи высотой h = q / g. Главные напряжения s1 являются большими. Для решения задачи воспользуемся условием прочности Кулона – Мора, записанным в форме соотношения главных напряжений:
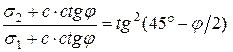 . (5.9)
. (5.9)
Решим уравнение (5.9) относительно давлений грунта на подпорную стену s2, для чего выполним следующие преобразования:
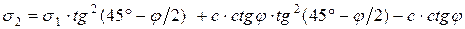 ;
;
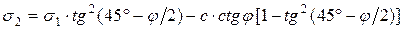 ;
;
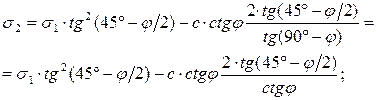
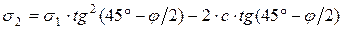 . (5.10)
. (5.10)
Предполагается, что вертикальные напряжения s1 от собственного веса грунта и веса пригруза на его поверхности изменяются по глубине грунтового массива как гидростатические давления, т. е. s1 = g ×(h + z), где g – удельный вес грунта. Тогда уравнения (5.10) примут окончательный вид:
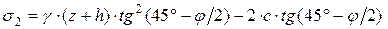 . (5.11)
. (5.11)
Напряжение s2 представляет собой искомое давление грунта на подпорную стену. Следующей задачей является определение равнодействующей Еa давлений s2 и плеча ее приложения ha. Давления по формуле (5.11) представляют собой линейную знакопеременную зависимость. Равнодействующую давлений Еa следует вычислять как площадь эпюры (5.11) в диапазоне положительных давлений, так как отрицательная площадь этой эпюры характеризует удерживающие силы, обусловленные силами сцепления грунта (второе слагаемое в формуле (5.11)). Для установления диапазона положительных давлений эпюры (5.11) в пределах высоты подпорной стены определим координату z0, соответствующую нулевому значению давления s2:
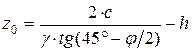 . (5.12)
. (5.12)
Формула (5.12) используется для определения глубины устойчивого котлована с вертикальными стенами, расположенного выше уровня грунтовых вод. Из этой формулы следует, что устройство котлована с вертикальными стенами в сыпучем грунте теоретически невозможно. Увеличение пригруза на бровке котлована приводит к уменьшению его устойчивой глубины (второе слагаемое в формуле (5.12)). Координата z0 по формуле (5.12) может быть как положительной, так и отрицательной. Физический смысл имеют значения 0 £ z0 £ H, где H – высота подпорной стены. При z0 < 0 диапазон положительных давлений распространяется в область пригруза (балласта), поэтому следует принимать z0 = 0. При z0 > Н положительные давления в пределах высоты стены отсутствуют (грунтовый массив устойчив), поэтому следует принимать z0 = Н. С учетом сделанных замечаний в отношении алгоритма вычисления координаты z0, сила давления на подпорную стену Еa (кН/м) может быть определена по формуле:
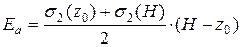 . (5.13)
. (5.13)
При вычислении силы давления по формуле (5.13) возникают определенные трудности в определении плеча ее приложения ha. Поэтому более предпочтительной является следующая интерпретация формулы (5.13):
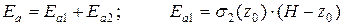 ;
;
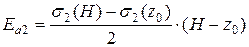 ;
;
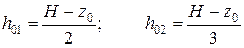 . (5.14)
. (5.14)
Представляют интерес частные случаи формул (5.13) и (5.14). Для идеально сыпучего грунта (с = 0) при отсутствии пригруза (h = 0) будем иметь:
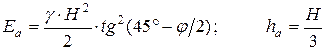 . (5.15)
. (5.15)
Для идеально связного грунта (j = 0) при отсутствии пригруза (h = 0) будем иметь:
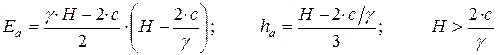 . (5.16)
. (5.16)
Давления по формулам (5.13) и (5.14) называются активными. Они реализуются, когда в состоянии предельного равновесия грунт перемещается относительно неподвижной конструкции. Таким образом, давление грунта на удерживающую его подпорную стену является активным давлением. Возможна другая форма предельного равновесия грунта, когда конструкция перемещается относительно неподвижного грунта. Такая форма предельного равновесия возникает за подпорной стеной (рис. 5.4) в массиве грунта, который удерживает подпорную стену от перемещений, вызванных активным давлением. Удерживающее подпорную стену напряжение в грунтовом массиве называется пассивным давлением. При определении пассивного давления учитывается, что горизонтальные напряжения s2 являются большими главными напряжениями. Тогда, по аналогии с выводом формул (5.10), будем иметь:

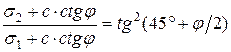 ;
;
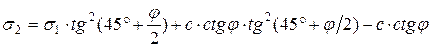 ;
;
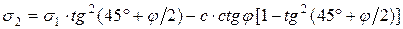 ;
;
 ;
;
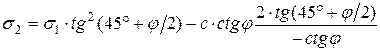 ;
;
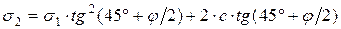 . (5.17)
. (5.17)
Принимая для вертикальных напряжений ранее установленную зависимость, получим окончательное выражение для пассивных давлений с учетом пригруза на поверхности грунта:
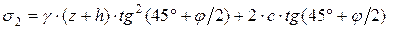 . (5.18)
. (5.18)
Эпюра пассивных давлений по всей высоте контакта конструкции с грунтом однозначна. Это упрощает выражение для силы Еп (кН/м) пассивного давления грунта:
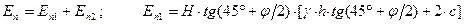 ;
;
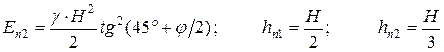 . (5.19)
. (5.19)
Для идеально сыпучего грунта (с = 0) при отсутствии пригруза (h = 0) Eп = Eп2. Для идеально связного грунта (j = 0) при отсутствии пригруза (h = 0) будем иметь:
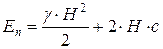 . (5.20)
. (5.20)
4. Устойчивость подпорных стен. Формами потери устойчивости подпорных стен (рис. 5.5) являются: сдвиг по подошве под воздействием активного давления грунта; опрокидывание относительно крайней точки на уровне подошвы со стороны, противоположной действию активного давления грунта. Проверка устойчивости подпорной стены выполняется с использованием двух уравнений равновесия: сумма проекций всех сил на горизонтальную ось равна нулю; сумма моментов всех сил относительно точки опрокидывания равна нулю.





|
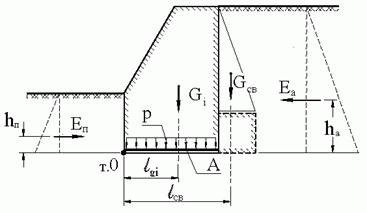
С учетом обозначений на рис. 5.5, эти проверки имеют вид:
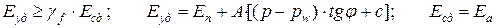 ;
;
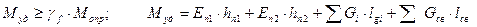 ;
;
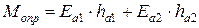 . (5.21)
. (5.21)
где А (кН/м) – погонная площадь подошвы подпорной стены; p, pw – соответственно среднее давление по подошве подпорной стены и поровое давление (при завершенной фильтрационной консолидации pw = 0);
Gi (кН/м), lgi – соответственно погонный вес части сечения подпорной стены и расстояние от центра тяжести этой части до точки опрокидывания;
Gсв, lсв – то же для грунта на свесах фундамента подпорной стены;
gf – коэффициент надежности по нагрузке, больший единицы.
 2015-03-07
2015-03-07 12461
12461
