Метод ветвей и границ. Идея этого метода состоит в последовательном ветвлении исходного множества решений на дерево подмножеств с нахождением решений на всех подмножествах пока не

Идея этого метода состоит в последовательном ветвлении исходного множества решений на дерево подмножеств с нахождением решений на всех подмножествах пока не получим искомое.

Как и методе отсекающих плоскостей, процесс начинается с решения задачи отбрасывая условие целочисленности. Если полученное решение не удовлетворяет условию целочисленности, то значение целевой функции дает верхнюю оценку искомого решения и начальное множество 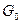. Если некоторая переменная не получила целочисленное значения, то в целочисленном плане ее либо следует уменьшить до 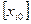либо увеличить до .

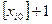Таким образом, исходное множество 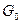разбиваем на два непересекающихся подмножества:

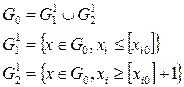
Находим решение и оценки на множествах. Если оба решения полученные на этих множествах оба целочисленны, то оптимальным будет то, у которого оценка больше. Если же, допустим на множестве 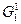получено целочисленное решение, а на 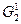- не целочисленное, но оценка второго множества больше чем оценка первого, то продолжаем ветвление множества 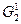, така как на следующем этапе мы можем получить целочисленное решение, оценка которого будет больше, чем оценка множества .

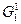Ветвление продолжается до тех пор пока не будет получено целочисленное решение с максимально большой оценкой.

ЛЕКЦИЯ 12.