Модель экономически обоснованных потребностей является широко известным способом расчета оптимального уровня производственных запасов. Основная идея этого способа изображена на рис. 23.1, где графически показаны различные издержки, связанные с обладанием производственными запасами (по вертикальной оси), по сравнению с величиной запасов (по горизонтальной оси). Как видно, вынужденные издержки возрастают, а издержки пополнения снижаются при увеличении размера производственных запасов. Исходя из нашего анализа издержек по предоставлению торгового кредита, можно увидеть, что общий вид графиков издержек кредитования и издержек по запасам примерно одинаков. С помощью модели EOQ мы постараемся определить точку минимальных издержек – Q*.
Перед тем, как начать обсуждение, сделаем одно замечание. Нам не важна точная величина издержек по запасам. Причиной этого является то, что суммарный объем производственных запасов, необходимых компании в течение года, определяется объемом продаж. Здесь мы постараемся выяснить, сколько запасов должно быть у компании в каждый отдельный промежуток времени. Или, более точно, мы постараемся определить, какой объем производственных запасов нужно дополнительно приобрести компании.
Истощение запасов. Чтобы разработать модель EOQ, сделаем предположение, что запасы компании равномерно убывают до тех пор, пока не закончатся, С этой точки зрения, компания должна поддерживать определенный уровень своих запасов. Например, предположим, что компания Eyssell имеет в наличии 3600 единиц определенного запаса, необходимых для производства конечного продукта. Годовые продажи этого продукта составляют 46800 единиц в год, т.е. 900 единиц каждую неделю. Таким образом, по истечении 4 недель запасы для производства этого продукта полностью истощатся и компании нужно будет сделать заказ поставщикам еще на 3 600 единиц, чтобы продолжить производство. Графическое изображение этого процесса расходования и пополнения производственных запасов будет напоминать по виду зубья пилы, что и показано на рис. 25.2. Как следует из графика, Eyssell всегда начинает производство, имея в наличии 3600 единиц готовой продукции в форме запасов, и заканчивает, имея в наличии 0. В среднем, вналичии находятся запасы, достаточные для производства 1800 единиц продукции, т.е. половины от начального объема.
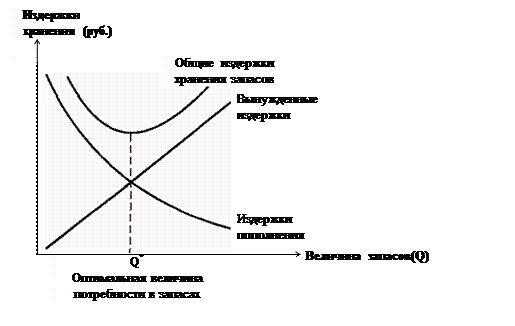
Рис. 25.1. Издержки хранения запасов
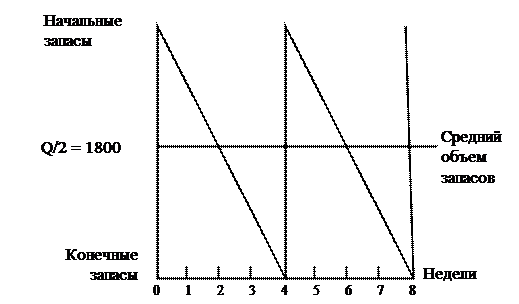
Рис. 25.2. Расходование и пополнение запасов в корпорации Eyssell
Вынужденные издержки. Как показано на рис. 25.1., вынужденные издержки обычно прямо пропорциональны объему запасов. Предположим, что объем запасов, которые Eyssell заказывает каждый раз, равно Q (3600 единиц). Назовем это объемом пополнения запасов. Средняя величина запасов тогда составит 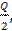 или 1800 единиц. Если мы определим вынужденные издержки на единицу готовой продукции в течение года равными СС, то тогда для компании Eyssell суммарные вынужденные издержки составят:
или 1800 единиц. Если мы определим вынужденные издержки на единицу готовой продукции в течение года равными СС, то тогда для компании Eyssell суммарные вынужденные издержки составят:
Суммарные вынужденные издержки = средняя величина запасов * вынужденные издержки на единицу продукции = 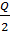 * СС (25.1.)
* СС (25.1.)
Для компании Eyssell, если вынужденные издержки равны 0,75 руб. на единицу готовой продукции в год, то суммарные вынужденные издержки можно определить умножением среднего объема запасов, 1800 единиц, на 0,75 руб., т.е. 1350 руб. в год.
Издержки масштабов производства. Теперь по л ностью сфокусируем наше внимание на издержках пополнения запасов. Мы сделаем допущение, что компания никогда не начинает производство при недостаточном количестве запасов, так что издержки по поддержанию необходимого количества запасов несущественны. Мы вернемся к этому вопросу позднее.
Издержки пополнения запасов, как правило, фиксированы. Другими словами, каждый раз, когда делается заказ поставщикам на поставку производственных запасов, это сопряжено с некоторыми фиксированными издержками (напомним, что стоимость самих запасов не рассматривается в данном примере). Определим объем продаж единиц готовой продукции в течение года буквой Т, Если компания заказывает Q единиц, необходимых для производства этой продукции запасов, то всего надо будет сделать 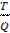 заказов. Для компании Eyssell годовой объем производства продукции составляет 46800 единиц, а каждый раз делается заказ на 3600 единиц, необходимых для производства этой продукции запасов. Таким образом, в течение года Eyssell делает 46800/3600 = 13 заказов. Если фиксированные издержки на один заказ составляют F, то общие издержки пополнения запасов в течение года составят:
заказов. Для компании Eyssell годовой объем производства продукции составляет 46800 единиц, а каждый раз делается заказ на 3600 единиц, необходимых для производства этой продукции запасов. Таким образом, в течение года Eyssell делает 46800/3600 = 13 заказов. Если фиксированные издержки на один заказ составляют F, то общие издержки пополнения запасов в течение года составят:
Общие издержки пополнения запасов = Фиксированные издержки на один заказ 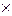 Число заказов =
Число заказов = 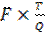 (25.2.)
(25.2.)
Для Eyssell, например, издержки на один заказ могут составлять 50руб., поэтому общие издержки пополнения запасов в случае 13 заказов будут равны:
50 руб. 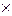 13 = 650руб. в год.
13 = 650руб. в год.
Суммарные издержки. Суммарные издержки, связанные с наличием у компании запасов, равны сумме вынужденных издержек и издержек пополнения запасов:
Суммарные издержки = Вынужденные издержки + Издержки пополнения запасов = 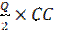 +
+ 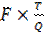 (25.3.)
(25.3.)
Нашей целью является определить значение Q, при котором эти суммарные издержки минимальны. Чтобы продемонстрировать то, как мы это сделаем, можно рассчитать значение суммарных издержек в зависимости от величины Q. Для компании Eyssell у нас есть следующие данные: вынужденные издержки (СС) равны 0,75 руб. на единицу продукции в год, фиксированные издержки (F) составляют 50 руб. за заказ, и общий объем продаж готовой продукции (Т) равен 46800 единиц в год. С помощью этих данных можно рассчитать возможные значения суммарных издержек (попробуйте для практики это сделать для некоторых значений) (табл. 25.1).
Таблица 25.1.
 2015-03-20
2015-03-20 1095
1095








