Любую совокупность вещественных чисел (v 1, v 2, …, vk), взятых в определенном порядке, можно рассматривать как точку или вектор с теми же координатами в пространстве k измерений (k -мерном пространстве). Запись вида v = (v 1, v 2, …, vk) обозначает точку или вектор v с указанными в скобках координатами [4]. Если для k -мерных векторов v и w справедливы основные алгебраические операции:
сложение и вычитание
v ± w = (v 1 ± w 1, v 2 ± w 2, …, vk ± wk),
умножение на действительное число u
u × v = (u × v 1, u× v 2, …, u × vk),
v × w = (v 1 × w 1, v 2 × w 2, …, vk × wk),
то совокупность всех таких векторов называют k -мерным евклидовым пространством и обозначают Ek.
Длиной вектора v называют число, определяемое по формуле
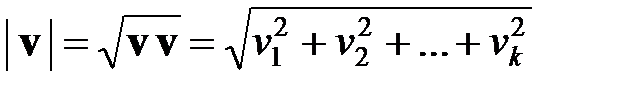 . . | (2.1) |
Длину вектора можно вычислить только тогда, когда компоненты вектора представлены в одной шкале измерений или они являются безразмерными величинами, полученными, например, в результате преобразования (1.1) – кодированные переменные безразмерны.
Если произведение v × w = 0 при | v | ≠ 0 и | w | ≠ 0, то векторы v и w являются ортогональными.
Единичным называют вектор, определяемый по формуле
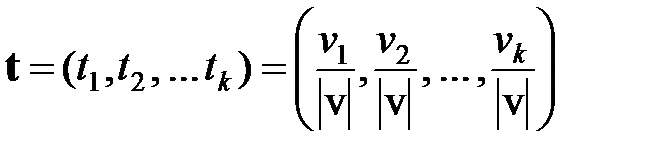 . . | (2.2) |
Пусть в Ek заданы некоторая точка V = (v 1, v 2, …, vk), единичный вектор t и непрерывно дифференцируемая по всем аргументам функция f (V) = f (v 1, v 2, …, vk).Производной в точке V от функции f (V) по направлению луча, определяемому вектором t, называется предел
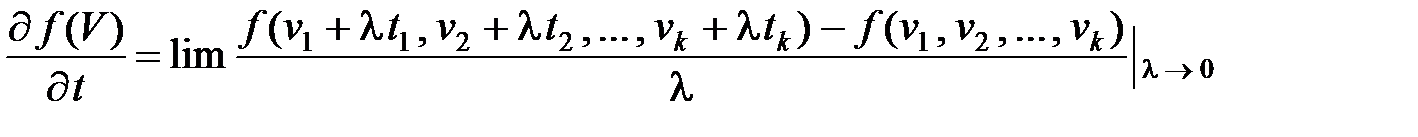 или
или
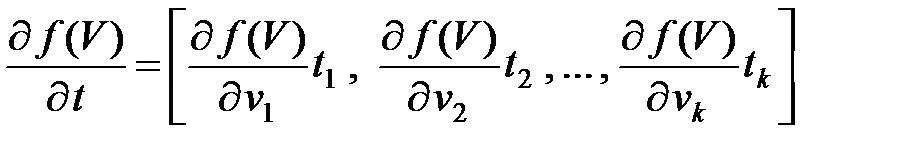 .
.
Градиентом функции f (V) называют вектор Ñ f (V) с координатами, равными частным производным по соответствующим аргументам
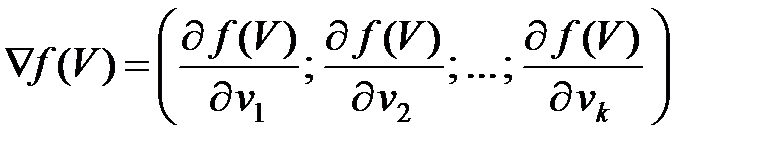 . . | (2.3) |
Градиент указывает направление наибольшего возрастания функции. Противоположное направление –Ñ f (V) называется антиградиентом, оно показывает направление наискорейшего убывания функции. В точке экстремума V* градиент равен нулю Ñ f (V* ) = 0. Если аналитически производные определить невозможно, их вычисляют приближенно ¶ f (V) / ¶ vi» D f (V) / D vi, где D f (V) – приращение функции f (V) при изменении аргумента на величину D vi. Двигаясь по градиенту (антиградиенту) можно достичь максимума (минимума) функции. В этом и состоит сущность градиентного метода оптимизации.
 2015-03-07
2015-03-07 1951
1951
