Т.к. производная по направлению является линейной частью прищения функции в данном направлении, то если градиент отличен от нуля в данной точке и направление движения образует острый угол с направлением градиента, то при достаточном малом сдвиге в этом направлении значение функции увеличивается, а при достаточно малом сдвиге в противоположном направлении – уменьшается.
Это свойство используется для последовательного улучшения значений непрерывного дифференцируемых функций при решении задач минимизации (максимизации), а соответствующие методы называемые релаксационными. Если движение производится точно в направлении градиента, то метод называется градиентным.
Различают градиентные методы I и II порядков. Градиент функции в некоторой точке это вектор, показывающий направление наибольшей скорости увеличения функции. Антиградиент –убывание функции (т.е. противоположно градиенту).
Grad 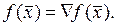 Если спроектировать его на ортогональные оси.
Если спроектировать его на ортогональные оси.
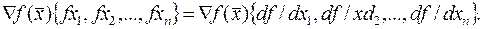
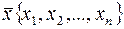 вектор сторка
вектор сторка
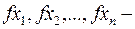 проекции градиента.
проекции градиента.
Антиградиент -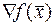 т.е. -
т.е. - 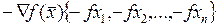
3. Метод наискорейшего спуска. (1-го порядка)
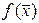 где
где 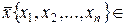 М откр.
М откр.
Алгоритм любого метода поиска отражается следующей поисковой формулой.
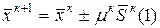 или
или 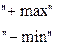
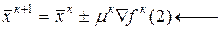
К –номер итерации;
S- направление, в котором осуществляется поиск;
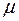 - величина шага.
- величина шага.
Знак ± 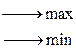

Ели движение по градиенту, то
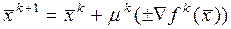
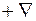 -градиент -
-градиент -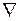 антиградиент часто пользуется
антиградиент часто пользуется
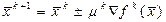
Пример.
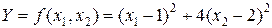
Начальная точка 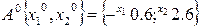 к=0
к=0
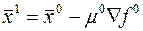
 2014-02-13
2014-02-13 1451
1451








