Линейное программирование

2.1 Теоретические сведения

Линейное программирование –это раздел математики, в ко­тором изучаются методы решения линейных задач оптимизации, иначе говоря, методы поиска минимума (или максимума) линей­ной функции при наличии линейных же ограничений[3]. Система ограничений может содержать и равенства и неравенства, то есть может быть смешанной. Однако с помощью введения дополни­тельных неизвестных она всегда может быть преобразована к одной из основных форм. Этих форм две.

Первая форма содержит только ограничения в виде равенств и обязательно условие не отрицательности всех неизвестных.

Вторая форма содержит только ограничения – неравенства, в числе которых могут быть (а могут и не быть) условия не отрицательности неизвестных.

Таким образом, формально произвольная задача линейного программирования может быть записана в виде:

Найти min 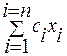при ограничениях: Ax=b

Dx <=d

Здесь x - неизвестный вектор с координатами x _i (i=1,2,…,n). n-число неизвестных. с - заданный вектор. Матрица A имеет не более n строк, а число строк матрицы D произвольно. Число столбцов в каждой из этих матриц равно n. Матрицы A и D и векторы b и d заданы.

Первая форма задачи линейного программирования имеет вид:

Найти min 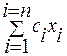_i при ограничениях: Ax=b и x_i >=0.

Перейти от произвольной задачи линейного программирования к основной форме можно с помощью введения дополнительных переменных. При этом каждое неравенство становится равенством и вместо не ограниченных по знаку переменных x _i вводятся неотрицательные переменные u _i и v _i (i=1,2,…n) по формуле

x _i = u _i - v _i.

Вторая форма задачи линейного программирования имеет вид:

Найти min Σ c _i x _i при ограничениях: Ax<=b.

i

К ней можно перейти путём замены каждого равенства двумя неравенствами противоположного знака. При этом увеличивается число ограничений, но остаются те же неизвестные.

Характерно, в каждой из основных форм записи задачи линейного программирования присутствуют ограничения - неравен-ства, в частности ограничения по знаку неизвестных, то есть неравенства вида x_i >=0 (i=1,…,n). Наличие ограничений в виде неравенств - это и есть та особенность задачи (не только в линейном случае), которая не позволяет применить для её решения аппарат классической математики: вычислить частные производные целевой функции, приравнять их нулю и после решения полученной системы уравнений найти стационарные точки и исследовать их на наличие экстремума. В задаче линейного программирования вообще частные производные целевой функции постоянны и их приравнивание к нулю не имеет никакого смысла.

Переход от произвольной системы ограничений к системе записанной в одной из основных форм необходим потому, что задачи линейного программирования при большом числе неизвестных решаются на компьютерах, а алгоритмы их решения и соответствующие компьютерные программы как раз и требуют записи задачи в соответствующей форме.

Для понимания методов решения задач линейного программирования необходимо знать свойства решений системы линейных неравенств, то есть структуру области допустимых решений. При этом решающее значение имеет линейность ограничений.

Программа DANTZIG_1 позволяет решать произвольную систему линейных неравенств с двумя неизвестными и получать графическое изображение не только окончательного решения, т.е. допустимой области, но и видеть процесс формирования этой области при вводе очередного ограничения. Поскольку с системой линейных неравенств приходится иметь дело не только в линейном программировании, но и при оптимизации нелинейных функций, образное восприятие различных ситуаций, возникающих при наличии различных линейных ограничений, имеет особое значение для понимания сущности широкого круга оптимизационных задач и методов их решения.

Программа DANTZIG_1 начинает выяснение свойств решений системы линейных неравенств с вопроса о том, что является решением одного отдельного неравенства, а затем переходит к системе неравенств. В заключение этого раздела она задаёт контрольные вопросы, в частности предъявляет различные варианты решений систем линейных неравенств (т.е. варианты допустимых областей) и спрашивает, возможны они или нет. Для ответов на эти вопросы необходимы знания высшей алгебры и математического анализа, полученные на 1-ом курсе.

Для иллюстрации различных ситуаций, возникающих при решении системы линейных неравенств, рассматривается двумерная задача, записанная во второй форме. Каждое неравенство даёт в качестве множества решений полуплоскость. А множество решений системы линейных неравенств либо пусто (система несовместна, рис. 3), либо неограничено (рис.4), либо представляет собой выпуклый многоугольник (на рис. 5 это треугольник) При числе неизвестных больше двух это выпуклый многогранник. Таким образом, наличие или отсутствие допустимых решений определяется системой органичений, а не целевой функцией.

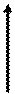x₂ x₂

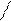
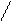
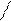
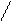
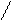
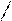
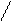
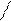
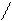
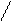
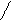
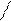
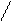
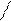
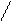
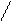
x₂ >=1

1

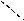
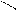
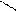
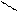
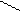
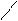
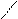
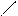
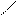
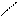
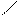
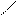
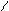
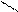
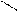
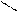
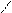
0 x₁ 0 x₁

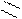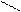
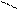
x₂ – x₁ <=0 x₂ + x₁ <= 0 x₂ – x₁ <=0 x₂ + x₁ <=0

Рис.3. Неравенства несовместны. Рис.4. Множество решений

не ограничено.

В случае неограниченной области допустимых решений существует направление (луч), по которому можно двигаться на неограниченное расстояние, оставаясь в пределах допустимой области. В ситуации, представленной на рис.4, из начала координат можно сколь угодно далеко идти по оси x₂ в отрицательном направлении. При этом оба неравенства x₂ – x₁ <=0 и x₂ + x₁ <=0 будут выполнены.

x₂ x₂ 1

1 0

-1

-2

0 x₁ 0 x₁

x₂ >= - 1 А B

A -1 B -1

x ₂+x₁ <=0

x₂ – x₁ <=0

-2

Рис.5. Допустимая область A0B. Рис. 6. Линии уровня.

Обучающая программа DANTZIG_2 даёт геометрическую интерпретацию поиска минимума (максимума) линейной функции на множестве решений системы линейных неравенств, т. е. на допустимой области. При этом используются линии уровня целевой функции, то есть такие линии, на каждой из которых целевая функция постоянна. В линейном программировании целевая функция линейна и линии уровня прямые (в многомерном случае это гиперплоскости). Каждой линии уровня соответствует своё значение целевой функции. Геометрический смысл задачи линейного программирования состоит в том, чтобы, не выходя за пределы допустимой области, найти точку на линии уровня с наименьшим значением (в задаче на поиск максимума с наибольшим значением).

На рис. 5 представлена допустимая область A0B, соответствующая системе линейных неравенств:

x₂ –x₁<=0

x₂ +x₁<=0

-x₂ <= 1

и различные линии уровня целевой функции F(x₁, x₂ )= x₂ – x₁

Если задача состоит в поиске точки минимума целевой функции, то это точка B(1,-1), так как она является допустимой и принадлежит линии уровня с наименьшим значением равным минус 2. Если же задача состоит в поиске точки максимума той же целевой функции на той же допустимой области, то таких точек бесконечно много (отрезок A0), но все они принадлежат линии уровня со значением нуль.

Если в качестве целевой функции взять - F(x₁, x₂)= x₁ – x₂, то точка минимума становится точкой максимума, а все точки максимума становятся точками минимума.

В теории линейного программирования доказано[3] (и обучающая программа DANTZIG_2 напоминает об этом), что, если точка минимума единственная, то это обязательно крайняя точка

(вершина) допустимой области, если же точек минимума бесконечно много, то все они лежат на одной линии уровня и среди них есть вершина (и не одна) с тем же самым значением целевой функции (рис.6). Таким образом, в задаче линейного программирования не может быть локальных минимумов и решение имеет смысл искать только среди крайних точек (вершин) допустимой области. Это существенно упрощает алгоритмы поиска решений.

В вершине допустимой области число ограничений, выполненных как равенства, равно числу неизвестных (при отсутствии вырожденности). Такие ограничения называются активными. Следует обратить внимание на то обстоятельство, что не каждый набор активных ограничений, число которых равно числу неизвестных, дает точку области допустимых решений. Другими словами, в вершине всегда активны ровно n ограничений, но другие ограничения при этом могут не выполняться, то есть не всякая вершина есть допустимая точка. Этот факт подчёркивается обучающей программой DANTZIG_2. Эта программа демонстрирует различные формы записи задачи, излагает основные идеи и демонстрирует алгоритм симплекс-метода на конкретной задаче, задает большое число тестовых вопросов по линейному программированию, что позволяет пользователю оценить свои знания в данной области.

Программа показывает, что число ограничений - неравенств может быть много больше числа неизвестных и из этих неравенств можно составить различные наборы (комбинации) по n неравенств в каждом. В отсутствие вырожденности каждый такой набор даёт только одну точку, удовлетворяющую всем неравенствам из этого набора, (иначе нет допустимых точек вообще), но эта точка (вершина) может не удовлетворять какому-нибудь из ограничений, не включённых в набор.

Так, в случае двух переменных (на плоскости) при большом числе неравенств область допустимых решений может представлять собой многоугольник с большим числом вершин. В каждой вершине (при отсутствии вырожденности) пересекаются только две ограничивающих прямых, то есть активны два ограничения, но при этом есть много точек пересечения других двух прямых, которые не являются допустимыми.

x₂ F

С D G

В Е

А

0 x₁

Рис. 7. Вершины A,B,C,D,E- допустимые,

F,G - не допустимые.

В линейном программировании вершины допустимой области играют особую роль, так как именно среди вершин нужно искать точку минимума.

Наиболее известный алгоритм поиска, реализует симплекс- метод, который состоит в том, что отправляясь от произвольной вершины допустимой области, осуществляется переход в другую вершину с меньшим значением целевой функции. Число вершин конечно, но при числе переменных и ограничений уже порядка сотен оно очень велико и слепой перебор невозможен даже на современных компьютерах. Однако симплекс – метод позволяет решать линейные задачи в приемлемое время и при числе переменных и ограничений в несколько тысяч именно из-за того, что на каждом шаге получается новая допустимая вершина с меньшим значением целевой функции.

Алгоритм симплекс – метода работает с симплексными таблицами. Обучающая программа DANTZIG_2 даёт эти таблицы для конкретной задачи и показывает соответствие очередной допустимой вершины и симплексной таблицы.

Освоение обучающих программ DANTZIG_1 и DANTZIG_2 должно предшествовать началу выполнения курсовой работы по линейному программированию. Особенно важно разобраться в тех вопросах, которые задают пользователю эти программы.