линейному программированию

По разделу Линейное программирование можно выбрать одну из трёх тем:

1. Область допустимых решений;

2. Симплекс метод;

3. Двойственные задачи линейного программирования.

При работе по первой теме необходимо изложить роль неравенств при решении задач оптимизации, изучить свойства решений системы линейных неравенств и возможные варианты структуры допустимой области. Соответствующие примеры демонстрирует обучающая программа DANTZIG_1.

Важно обратить внимание на вопросы обучающей программы о том может ли допустимая область содержать только одну или только две точки и обосновать выбор вариантов допустимых областей из предлагаемых программой.

Самостоятельно необходимо привести примеры систем линейных неравенств относительно двух неизвестных и соответствующих областей допустимых решений для следующих случаев:

- допустимая область ограничена и представляет собой выпуклый многоугольник;

- допустимая область неограниченна;

- допустимая область пуста (ограничения несовместны).

Допустимые области следует изобразить графически.

В работе целесообразно объяснить: почему допустимая область это выпуклое множество и следовательно в случае двух переменных соответствующий ей многоугольник тоже выпуклый.

При работе по второй теме необходимо уяснить геометрический смысл задачи, особую роль крайних точек (вершин) допустимой области. Это наглядно демонстрирует обучающая программа DANTZIG_2.

Целесообразно проработать соответствующий раздел обучающей программы DANTZIG_2 и обосновать ответы на её вопросы о линиях уровня, о возможности решения задачи на неограниченной допустимой области, о локальных минимумах и бесконечном множестве решений, о внутренних точках. На каждую иллюстрацию (пример), предлагаемую обучающей программой, следует привести свою, соответствующую конкретному случаю систему ограничений и целевую функции и изобразить графически линии уровня и многоугольник (допустимую область).

После изложения основных идей симплекс – метода следует взять конкретную задачу линейного программирования, которую рассматривает обучающая программа, и решить её самостоятельно с помощью симплекс- метода. Затем сопоставить симплексные таблицы с их аналогами из обучающей программы (должно быть совпадение и таблиц и результата).

Не следует ограничиваться одной задачей и привести в отчёте по курсовой работе по крайней мере решение двух задач, обратив внимание на получение допустимого начального приближения.

Учесть, что возможна неоднозначность в выборе разреша-ющего столбца симплексной таблицы и разрешающего элемента при уже выбранном разрешающем столбце [5]. Ответить на вопрос к чему может привести эта неоднозначность?

При выборе для курсовой работы третьей темы: Двойственные задачи линейного программирования необходимо иметь в виду что задачи линейного программирования обладают особым свойством двойственности, состоящим в том, что для каждой задачи можно по определенным правилам построить другую задачу линейного программирования и, решив ее, найти экстремум исходной задачи (значение целевой функции).

Если исходная (прямая) задача записана в первой основной форме: найти

min 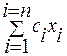при ограничениях: Ax = b и x_i >= 0 (i = 1, …, n),

то двойственная задача имеет следующий вид:

найти max 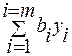при ограничениях: A^Ty <= c.

Здесь m — число строк матрицы А, а А^Т — транспонированная матрица А. Заметим, что здесь ограничения y _i >= 0 (i = 1, …, m) отсутствуют и двойственная задача представлена во второй основной форме. Вместо min имеем max, векторы b и c поменялись местами, уравнения стали неравенствами.

Если исходная задача имеет решение, то двойственная тоже имеет решение, и ее максимум численно равен минимуму исходной задачи. Число переменных в двойственной задаче равно числу ограничений-равенств исходной задачи, которое всегда меньше числа переменных исходной задачи. Число ограничений-неравенств двойственной задачи равно числу переменных исходной задачи, но, поскольку ограничения по знаку в двойственной задаче отсутствуют, то суммарно число ограничений в двойственной задаче меньше, чем в исходной.

Если исходная задача записана в виде: найти

min 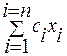при ограничениях: Ax < = b и x _i >= 0 (i = 1, …, n),

то двойственная задача имеет вид: найти max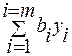

при ограничениях: A^Ty >= c и y_i >= 0 (i = 1, …, m).

Двойственность взаимна, т.е. полученную задачу можно рассматривать как исходную, а исходную как двойственную к ней. Если ставится цель найти экстремум целевой функции, а точка, в которой он достигается, не нужна, то переход к двойственной задаче в ряде случаев может быть оправдан.

Решив двойственную задачу, мы получаем экстремальное значение целевой функции, но не точку (значения переменных исходной задачи), в которой достигается экстремум.

В отчёте по курсовой работе следует привести конкретные примеры решения прямой и двойственной задач линейного программирования.

Кроме того, курсовая работа может быть выполнена на тему Многоэкстремальные задачи. При её выполнении следует рассмотреть методы сведения многокритериальных задач к однокритериальным, множества Парето и их применение при решении некоторых задач распределения ресурса.

Библиографический список.

1. Беллман Р. Динамическое программирование. - М: ИЛ, 1960

2. Беллман Р., Дрейфус С. Прикладные задачи динамического программирования.- М.: Наука, 1964

3. Вентцель Е.С. Исследование операций. Задачи, принципы, методология.- М.: Наука, 1980

4. Хедли Дж. Нелинейное и динамическое программирование.-М: Мир, 1967

5. Струченков В.И. Методы оптимизации. Основы теории, задачи, обучающие компьютерные программы.- М: Солон- Пресс, 2007