| Сравнение | 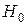
| Статистика критерия | 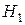
| Область принятия 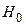
|
| генеральных средних | 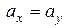
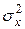 и и 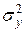 известны
известны
| 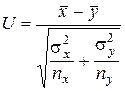
| 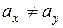
| 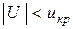 , ,
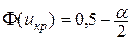
|
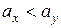
| 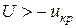 , ,
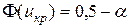
| |||
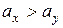
| 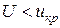 , ,
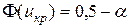
| |||
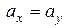
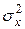 и и 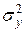 неизвестны,
но равны
неизвестны,
но равны
| 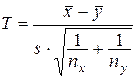 , ,
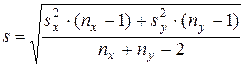 Если принимается
Если принимается 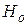 , то генеральная средняя оценивается величиной: , то генеральная средняя оценивается величиной: 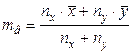
| 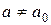
| 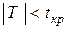 , ,
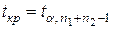 для двусторонней области
для двусторонней области
| |
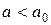
| 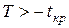 , ,
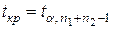 для односторонней области
для односторонней области
| |||
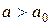
| 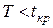 , ,
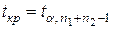 для односторонней области
для односторонней области
| |||
| генеральных дисперсий | 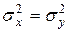
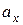 и и 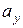 неизвестны
неизвестны
| 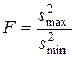 Если принимается
Если принимается 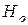 , то генеральная дисперсии оценивается величиной: , то генеральная дисперсии оценивается величиной:
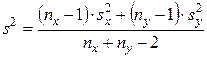
| 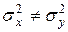
| 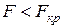 , ,
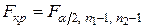
|
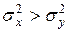
| 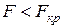 , ,
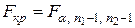
| |||
| генеральных долей признака | 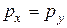
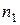 и и 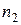 достаточно
большие
достаточно
большие
| 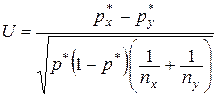 , ,
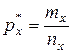 , , 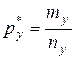
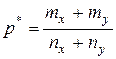
| 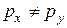
| 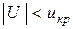 , ,
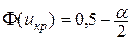
|
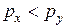
| 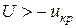 , ,
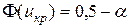
| |||
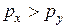
| 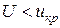 , ,
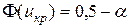
|
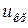 − аргумент функции Лапласа;
− аргумент функции Лапласа; 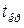 − распределение Стьюдента;
− распределение Стьюдента;
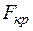 − распределение Фишера–Снедекора.
− распределение Фишера–Снедекора.
 2015-03-20
2015-03-20 361
361








