1. ГИПОТЕЗЫ. ПОСТАНОВКА ВОПРОСА
Так как на основе статистического материала вычисляются лишь оценки истинных параметров распределения, то встаёт вопрос о значимости расхождений между статистическими вычислениями и действительностью.
· Статистической гипотезой (или просто гипотезой) называется любое предположение о генеральной совокупности, проверяемое по выборке.
· Нулевой гипотезой – 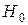 называют гипотезу, выдвигаемую в качестве основной, которая отвергает значимость расхождений.
называют гипотезу, выдвигаемую в качестве основной, которая отвергает значимость расхождений.
· Альтернативной (конкурирующей) гипотезой 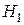 называется гипотеза, которая противоречит нулевой гипотезе
называется гипотеза, которая противоречит нулевой гипотезе 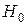 .
.
· Процедура сопоставления высказанного предположения (гипотезы) с выборочными данными называется проверкой гипотез.
Так как решение о справедливости гипотезы принимается на основании выборочных данных, то могут возникать ошибки двух родов.
| Ошибка I рода | Ошибка II рода |
| Отвергается основная (нулевая) гипотеза, хотя она верна. | Отвергается конкурирующая гипотеза, хотя она верна. |
Вероятность ошибки: 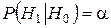 , ,
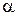 – уровень значимости критерия (обычно – уровень значимости критерия (обычно 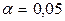 ; 0,01; 0,005; 0,001). ; 0,01; 0,005; 0,001).
| Вероятность ошибки: 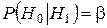 (величина
(величина 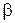 , как правило, заранее неизвестна) , как правило, заранее неизвестна)
|
Вероятность принять верную (нулевую) гипотезу: 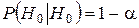 . .
| Вероятность принять верную (конкурирующую) гипотезу:
 , ,
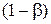 – мощность критерия. – мощность критерия.
|
Последствия ошибок 1-го и 2-го рода могут быть абсолютно различными: в одних случаях надо минимизировать 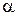 , а в других –
, а в других – 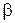 . Так, применительно к радиолокации говорят, что
. Так, применительно к радиолокации говорят, что 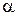 – вероятность пропустить сигнал,
– вероятность пропустить сигнал, 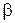 – вероятность ложной тревоги. Применительно к производству, к торговле можно сказать, что
– вероятность ложной тревоги. Применительно к производству, к торговле можно сказать, что 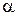 – риск поставщика (т. е. забраковка всей партии изделий, удовлетворяющих стандарту),
– риск поставщика (т. е. забраковка всей партии изделий, удовлетворяющих стандарту), 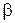 – риск потребителя (т. е. приём по выборке всей партии изделий, не удовлетворяющих стандарту). Применительно к судебной системе, ошибка 1-го рода приводит к оправданию виновного, ошибка 2-го – осуждение невиновного.
– риск потребителя (т. е. приём по выборке всей партии изделий, не удовлетворяющих стандарту). Применительно к судебной системе, ошибка 1-го рода приводит к оправданию виновного, ошибка 2-го – осуждение невиновного.
Следует отметить, что одновременное уменьшение ошибок 1-го и 2-го рода возможно лишь при увеличении объёма выборок. Поэтому обычно при заданном уровне значимости 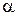 отыскивается критерий с наибольшей мощностью.
отыскивается критерий с наибольшей мощностью.
· Правило, по которому принимается решение принять или отклонить гипотезу 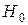 , называется статистическим критерием (критерием) проверки гипотезы
, называется статистическим критерием (критерием) проверки гипотезы 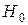 .
.
· Статистикой (тестом) называют СВ 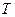 , которая служит для проверки гипотезы.
, которая служит для проверки гипотезы.
· Критической областью 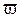 называют совокупность значений статистики
называют совокупность значений статистики 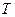 , при которых нулевая гипотеза отвергается.
, при которых нулевая гипотеза отвергается.
· Критическими точками 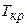 называют точки, отделяющие критическую область от области принятия нулевой гипотезы.
называют точки, отделяющие критическую область от области принятия нулевой гипотезы.
СВ 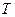 имеет симметричный закон распределения с математическим ожиданием, равным нулю. Положительные значения
имеет симметричный закон распределения с математическим ожиданием, равным нулю. Положительные значения 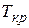 табулированы с учётом уровня значимости.
табулированы с учётом уровня значимости.
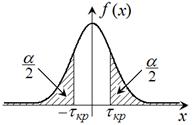
Различают три типа критической области:
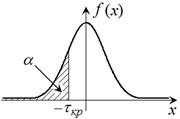
| 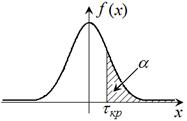
| 
|
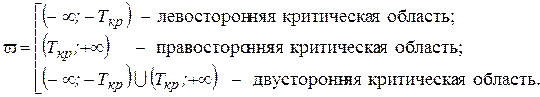
Если 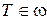 , то нулевую гипотезу следует отвергнуть (принимается альтернативная гипотеза). При этом может быть совершена ошибка I–ого рода:
, то нулевую гипотезу следует отвергнуть (принимается альтернативная гипотеза). При этом может быть совершена ошибка I–ого рода: 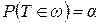 .
.
 2015-03-20
2015-03-20 585
585








