Проверка гипотез о законе распределения

Как бы хорошо ни был выбран теоретический закон распределения, неизбежны расхождения между эмпирическим и теоретическим распределениями. Естественно, возникает вопрос: эти расхождения объясняются только случайными обстоятельствами, связанными с небольшим числом наблюдений, или они являются существенными и связаны с тем, что теоретический закон распределения подобран неудачно. Для ответа на этот вопрос используем специально подобранную величину – критерийсогласия.

· Критерием согласия называют статистический критерий проверки гипотезы о предполагаемом законе неизвестного распределения.

Пусть необходимо проверить гипотезу 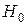о том, что рассматриваемая СВ Х подчиняется определённому закону распределения. Для проверки гипотезы 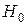выбирают некоторую СВ 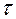, характеризующую степень расхождения теоретического и эмпирического распределений, закон распределения которой при достаточно больших п известен и практически не зависит от закона распределения случайной величины Х.

Зная закон распределения 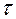, можно найти такое критическое значение 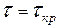, что если гипотеза 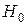верна, то вероятность того, что 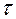приняла значение больше чем 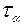: 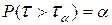– мала, где 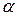– уровень значимости критерия.

Если наблюдаемое в опыте значение 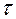окажется больше критического: 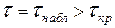(т. е. попадёт в критическую область), то в соответствии с принципом практической уверенности это означает, что такие большие значения практически 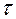невозможны и противоречат гипотезе 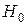. В этом случае нулевую гипотезу отвергают.

Если 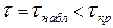, то расхождение между эмпирическим и теоретическим распределениями несущественно и гипотезу 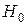можно считать правдоподобной или, по крайней мере, не противоречащей опытным данным.

Существуют различные критерии согласия: Пирсона, Колмогорова, Фишера, Смирнова и др.