· Эмпирические кратности – это кратности 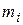 , наблюдаемые в эксперименте.
, наблюдаемые в эксперименте.
· Выравнивающие кратности – это кратности, которые находятся по формуле 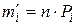 ,
,
где 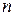 –объём выборки,
–объём выборки,
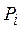 – точечная вероятность варианты
– точечная вероятность варианты 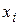 дискретной СВ или интервальная вероятность для варианты
дискретной СВ или интервальная вероятность для варианты 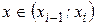 непрерывной СВ.
непрерывной СВ.
Алгоритм действий:
1. Выбрать закон распределения СВ и для него по эмпирическим характеристикам найти теоретическую дифференциальную функцию 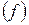 .
.
2. По соответствующей формуле вычислить точечную (или интервальную) вероятность 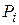 .
.
3. Вычислить выравнивающие кратности 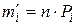 , где
, где 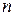 –объём выборки.
–объём выборки.
4. Найти статистику 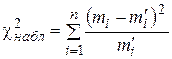 .
.
5. Определить число  ,
,
где 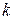 –число частичных интервалов выборки;
–число частичных интервалов выборки;
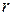 –число параметров дифференциальной функции распределения.
–число параметров дифференциальной функции распределения.
В частности:
| Биномиальный закон распределения СВ | 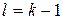 , если , если 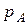 известно известно
|
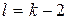 , если , если 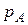 неизвестно неизвестно
| |
| Закон распределения Пуассона | 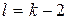
|
| Равномерный закон распределения СВ | 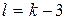
|
| Показательный закон распределения СВ | 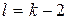
|
| Нормальный закон распределения СВ | 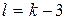
|
6. По таблице найти величину 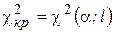 , где
, где 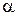 – уровень значимости.
– уровень значимости.
· Если 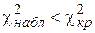 , то закон теоретического распределения выбран правильно.
, то закон теоретического распределения выбран правильно.
 2015-03-20
2015-03-20 503
503








