· Функциональная зависимость каждому значению одной переменной ставит в соответствие вполне определённое единственное значение другой. Когда каждому значению одной величины соответствует множество возможных значений другой величины, то зависимости относятся к корреляционным.
· Зависимость называется статистической если изменение одной СВ влечёт изменение другой СВ.
· Статистическую зависимость называют корреляционной, если изменение одной СВ влечёт изменение среднего значения другой СВ.
Имеется две СВ 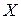 и
и 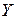 . При большом числе наблюдений одно и то же значение х может встретиться
. При большом числе наблюдений одно и то же значение х может встретиться 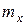 раз, одно и то же значение у –
раз, одно и то же значение у – 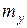 раз, одна и та же пара чисел
раз, одна и та же пара чисел 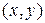 может наблюдаться
может наблюдаться 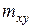 раз. Поэтому данные наблюдений группируют, т. е. подсчитывают частоты
раз. Поэтому данные наблюдений группируют, т. е. подсчитывают частоты 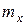 ,
, 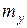 ,
, 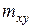 . Все сгруппированные данные записывают в виде таблицы, которую называют корреляционной:
. Все сгруппированные данные записывают в виде таблицы, которую называют корреляционной:
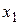
| 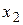
| … | 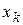
| 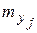
| |
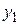
| 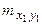
| 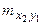
| 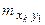
| 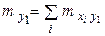
| |
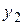
| 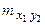
| 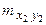
| 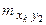
| 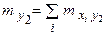
| |
| … | |||||
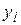
| 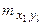
| 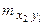
| 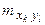
| 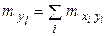
| |
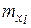
| 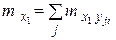
| 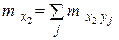
| 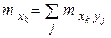
| 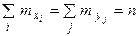
|
где 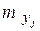 – частота появления варианты
– частота появления варианты 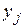 ,
,
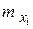 – частота появления варианты
– частота появления варианты 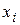 ,
,
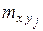 – частота появления варианты
– частота появления варианты 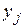 при заданном значении варианты
при заданном значении варианты 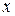 ,
,
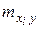 – частота появления варианты
– частота появления варианты 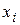 при заданном значении варианты
при заданном значении варианты 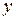 ,
,
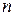 – объём выборки.
– объём выборки.
Определим некоторые первичные понятия:
Для СВ 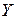
| Для СВ 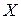
|
| Общее среднее | |
– это среднее арифметическое всех значений СВ 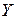 : : 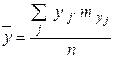
| − это среднее арифметическое всех значений СВ 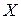 : : 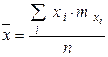
|
| Условное среднее | |
− это среднее арифметическое тех значений СВ 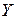 , которые соответствуют значению СВ , которые соответствуют значению СВ 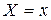 : :
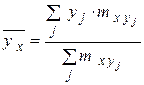
| − это среднее арифметическое тех значений СВ 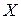 , которые соответствуют значению СВ , которые соответствуют значению СВ 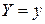 : :
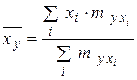
|
| Межгрупповое среднее | |
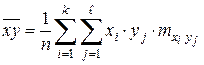
| |
| общее среднее квадратическое отклонение | |
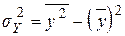
| 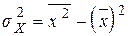
|
| межгрупповое среднее квадратическое отклонение | |
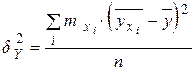
| 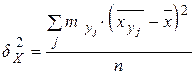
|
Пример. Сгруппированные данные внесены в таблицу:
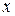
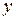
| 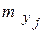
| ||
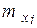
|
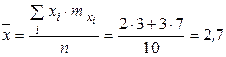 ;
; 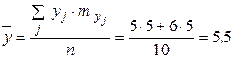 ;
;
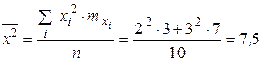 ;
; 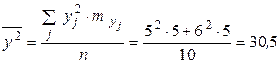 ;
;
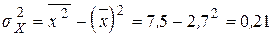 ;
; 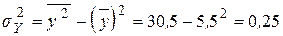 ;
;
 ;
; 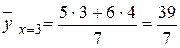 ;
;
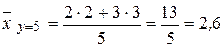 ;
; 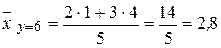 ;
;
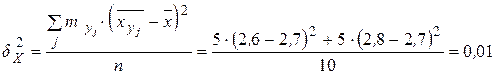 ;
;
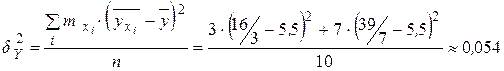 ;
;
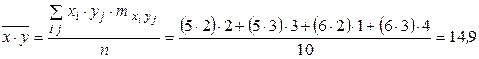 .
.
Вычисленные групповые средние 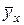 (и
(и 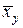 ) можно изобразить графически в виде ломаной, называемой эмпирической линией регрессии Y по Х (Х по Y).
) можно изобразить графически в виде ломаной, называемой эмпирической линией регрессии Y по Х (Х по Y).
· Уравнение, определяющее корреляционную зависимость 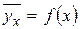 , называют уравнением регрессии СВ
, называют уравнением регрессии СВ 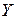 на СВ
на СВ 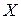 .
.
· 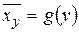 − уравнение регрессии СВ
− уравнение регрессии СВ 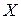 на СВ
на СВ 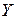 .
.
· Если обе функции регрессии 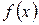 и
и 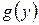 линейны, то корреляционную зависимость называют линейной.
линейны, то корреляционную зависимость называют линейной.
 2015-03-20
2015-03-20 406
406








