Пусть некоторая двумерная генеральная совокупность распределена нормально и из неё извлечена выборка объёма 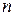 , для которой найдено значение
, для которой найдено значение 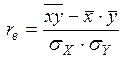 .
.
Проверяют нулевую гипотезу 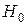 :
:
«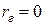 − линейная зависимость в генеральной совокупности отсутствует»
− линейная зависимость в генеральной совокупности отсутствует»
при выдвигаемой альтернативной гипотезе 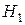 :
:
«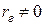 − линейная зависимость присутствует».
− линейная зависимость присутствует».
Алгоритм: 1. Вычислить статистику 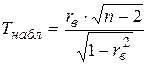 .
.
2. Определить критическое значение распределения Стьюдента 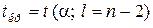 . Критической областью при этом является двусторонняя область
. Критической областью при этом является двусторонняя область 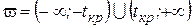 .
.
3. Сделать вывод:
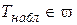 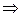 | гипотезу 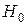 отвергают, т. е. имеется линейная зависимость; отвергают, т. е. имеется линейная зависимость; |
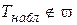 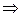 | гипотезу 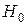 принимают, т. е. линейной зависимости нет. принимают, т. е. линейной зависимости нет. |
3.2 ПОИСК УРАВНЕНИЯ СВЯЗИ
А) Различные значения СВ X и соответствующие значения СВ Y наблюдались по одному разу. В результате 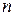 испытаний получены выборочные пары чисел
испытаний получены выборочные пары чисел
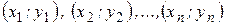 ,
,
которые располагаются на графике вдоль некоторой прямой 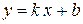 .
.
· Угловой коэффициент прямой линии регрессии 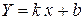 называют выборочным коэффициентом регрессии
называют выборочным коэффициентом регрессии 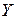 на
на 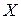 и обозначают:
и обозначают: 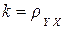 .
.
Неизвестные параметры 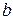 и
и 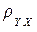 найдём методом наименьших квадратов.
найдём методом наименьших квадратов.
Составим функцию: 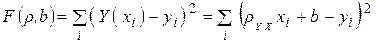
и решим систему относительно её частных производных:
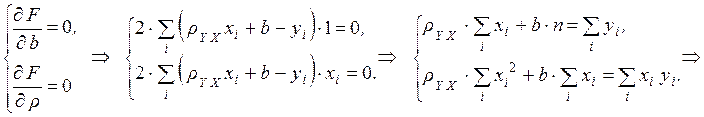
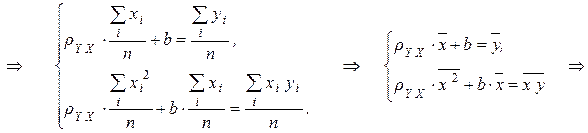
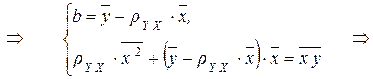
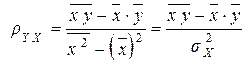 .
.
В итоге уравнение прямой линии регрессии примет вид:
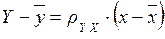 , где
, где 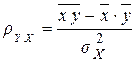 .
.
В) Сгруппированные значения СВ X и соответствующие значения СВ Y. В результате 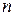 испытаний получены выборочные пары чисел
испытаний получены выборочные пары чисел 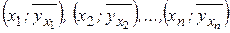 , которые располагаются на графике вдоль некоторой прямой линии регрессии
, которые располагаются на графике вдоль некоторой прямой линии регрессии 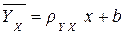 .
.
Проводя рассуждения по методу НК, получим уравнение:
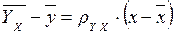 , где
, где 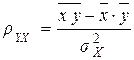 .
.
Видоизменим полученную зависимость.
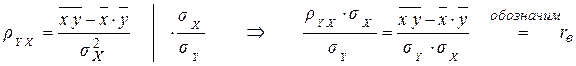 ;
;
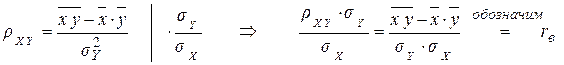 .
.
Получили систему: 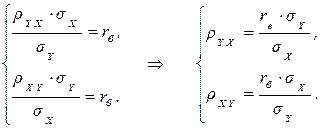
В итоге уравнение прямой линии регрессии примет вид:

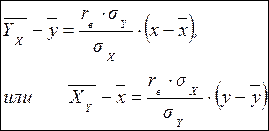 , где
, где 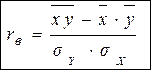 .
.
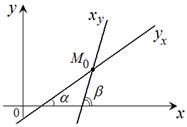 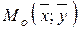 – точка пересечения двух линий регрессий. Для регрессии – точка пересечения двух линий регрессий. Для регрессии 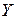 на на 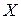 угловой коэффициент: угловой коэффициент: 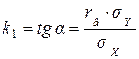 ; для регрессии ; для регрессии 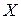 на на 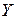 : : 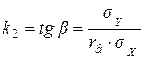 . . |
 2015-03-20
2015-03-20 2009
2009
