Введённый коэффициент 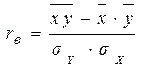 является характеристикой линейности уравнения регрессии.
является характеристикой линейности уравнения регрессии.
При этом: 
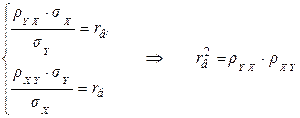
· Выборочным коэффициентом корреляции переменных 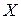 и
и 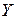 , между которыми предполагается линейная корреляционная связь, называется среднее геометрическое их коэффициентов регрессии и имеющее знак последних:
, между которыми предполагается линейная корреляционная связь, называется среднее геометрическое их коэффициентов регрессии и имеющее знак последних: 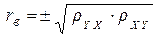 .
.
| Свойства коэффициента корреляции: | 1. 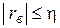 . .
|
2. 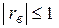 . .
|
Значения 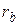
| Зависимость СВ 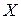 и и 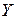
|
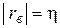
| Точная линейная корреляционная зависимость. |
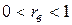
| Прямая связь линейной зависимости (возрастающая функция). |
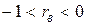
| Обратная связь линейной зависимости (убывающая функция). |
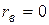
| Отсутствует линейная зависимость (графики уравнений регрессий взаимно перпендикулярны). |
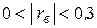
| Линейная зависимость практически отсутствует. |
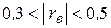
| Слабая линейная зависимость |
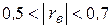
| Умеренная линейная зависимость. |
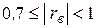
| Сильная линейная зависимость |
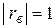
| Функциональной линейной зависимостью (графики уравнений регрессий совпадают). |
 2015-03-20
2015-03-20 452
452








