Случайные процессы с независимыми сечениями

В гидрологической практике гипотеза о том, что ряд соответствует модели случайной величины, принимается, если отсутствует значимая корреляция между членами этого ряда при любом сдвиге t. Однако в этом случае можно применить и модель случайного процесса с независимыми сечениями.

Случайный процесс называется случайным процессом с независимыми сечениями, если для любых значений t и t^' (t ¹ t^') корреляционная функция K_x (t, t^')равна нулю.

Этот процесс имеет следующие характеристики:

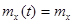, (6.65)

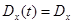, (6.66)

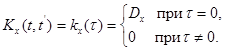(6.67)

Таким образом, этот процесс является стационарным и обладает эргодическим свойством. Для таких процессов характеристики одномерного закона распределения можно оценить как по любому сечению, так и по любой (достаточно продолжительной) реализации. У таких процессов отсутствует корреляция, как между сечениями, так и между членами внутри любой реализации.

Принимая эту модель, мы рассматриваем ряд гидрологических величин не как выборку из генеральной совокупности, а как одну реализацию случайного процесса.

Ситуация, когда приходится исследовать всего одну реализацию случайного процесса, встречается довольно часто. В этом случае реализацию иногда называют временным рядом, а при независимости сечений – временным рядом с независимыми значениями.

Очевидно, что если речь идет об описании статистической структуры одного ряда, эта модель мало отличается от модели обычной случайной величины. Поэтому в гидрологической литературе модель ряда в виде случайной величины и в виде случайного процесса с независимыми сечениями иногда рассматриваются как тождественные. При этом следует понимать, что для случайного процесса с независимыми сечениями корректно говорить о таких характеристиках как корреляционная функция и спектр, а для случайной величины – нет.

Корреляционная функция и спектральная плотность случайного процесса с независимыми сечениями имеет очень специфический вид, и являются мало информативными. В частности, спектральная плотность такого случайного процесса является постоянной для любого конечного интервала разложения:

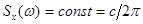. (6.68)

В то же время эмпирическая оценка спектральной плотности по любой произвольно взятой реализации будет представлять собой беспорядочные всплески случайным образом разбросанные по всему спектру частот со средним (по множеству реализаций) значением с /2p.

Случайный процесс с независимыми сечениями иногда называют "белым шумом" по аналогии с белым светом, у которого спектральный состав примерно однороден. При этом величину с называют интенсивностью белого шума.