Нормальные (Гауссовские) случайные процессы

Нормальным (гауссовским) случайным процессом X (t) называется случайный процесс, у которого во всех сечениях случайная величина X (t_i) имеет нормальное распределение.

Нормальный случайный процесс обладает рядом замечательных свойств.

§ Двумерный закон распределения нормального случайного процесса X (t) является его исчерпывающей характеристикой, так как все характеристики его n -мерного закона распределения зависят то двух функций – математического ожидания m_x (t) и корреляционной функции K_x (t,t^').

§ Если для нормального случайного процесса выполняется условие

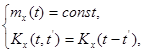(6.69)

то есть если он является стационарным в широком смысле, то он будет стационарным и в узком смысле; кроме того, он будет эргодическим.