Система координат на плоскости

Под системой координат на плоскости понимают способ, позволяющий численно описать положение точки плоскости. Одной из таких систем является прямоугольная (декартова) система координат.

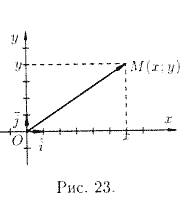Прямоугольная система координат задается двумя взаимно перпендикулярными прямыми — осями, на каждой из которых выбрано положительное направление и задан единичный (масштабный) отрезок. Единицу мас­штаба обычно берут одинаковой для обеих осей. Эти оси называют осями координат, точку их пересечения О - началом координат. Одну из осей называют осью абсцисс (осью Ох), другую — осью ординат (осью Оу) (рис. 23).

На рисунках ось абсцисс обычно располагают горизонтально и направленной слева направо, а ось ординат - вертикально и направленной снизу вверх. Оси координат делят плоскость на четыре области — четверти (или квадранты).

Единичные векторы осей обозначают i и j (| i |=| j |=1, 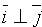). Систему координат обозначают Оху, а плоскость, в которой расположена

система координат, называют координатной плоскостью.

Рассмотрим произвольную точку Μ плоскости Оху. Вектор ОМ называется радиусом-вектором точки М.

Координатами точки Μ в системе координат Оху называ­ются координаты радиуса-вектора OM. Если OM=(x;y), то координаты точки Μ записывают так: М(х;у), число x называется абсциссой точки М, у — ординатой точки Μ.

Эти два числа x и y полностью определяют положение точки на плоскости, а именно: каждой паре чисел x и y соответствует единственная точка М плоскости, и наоборот.

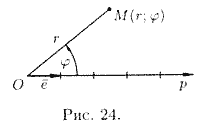
Другой практически важной системой координат является полярная система координат. Полярная система координат задается точкой О, на­зываемой полюсом, лучом Ор, называемым полярной осью, и единичным вектором e того же направления, что и луч Ор.

Возьмем на плоскости точку М, не совпадающую с О. Положение точки М определяется двумя числами: ее расстоянием г от полюса О и углом φ, образован­ным отрезком ОМ с полярной осью (отсчет углов ведет­ся в направлении, противоположном движению часовой стрелки) (см. рис. 24).

Числа r и φ называются полярными координатами точки М, пишут М(r; φ), при этом r называют полярным радиусом, φ — полярным углом.

Для получения всех точек плоскости достаточно полярный угол φ ограничить промежутком (—π; π] (или 0< φ < 2πr), а полярный радиус — [0;∞). В этом случае каждой точке плоскости (кроме О) соответствует единственная пара чисел r и φ, и обратно.

Установим связь между прямоугольными и полярными координатами. Для этого совместим полюс О с началом координат системы Оху, а полярную ось — с положительной полуосью Ох. Пусть x и у — прямоугольные координаты точки М, а r и φ — ее полярные координаты.

Из рисунка 25 видно, что прямоугольные координаты точки М выражаются через полярные координаты точки следующим образом:

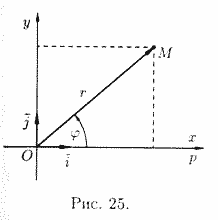
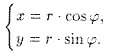
Полярные же координаты точки М выражаются через ее декартовы координаты (тот же рисунок) такими формулами

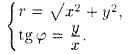
Определяя величину φ, следует установить (по знакам x и у) четверть, в которой лежит искомый угол, и учитывать, что -π < φ< π.

Основные приложения метода координат на плоскости