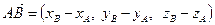(см.учебно-методическое пособие, автор Ваксман К.Г.)
Контрольная работа №1г содержит 4 задания.
Краткие теоретические сведения.
I. Элементы аналитической геометрии.
1) Прямоугольная декартова система координат образуется двумя взаимно перпендикулярными прямыми, на которых выбрано направление и масштаб.
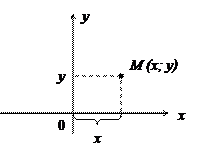 | |||
| |||
2) Полярная система координат задаётся полупрямой – полярной осью с выбранным масштабом и направлением
Положение точки на плоскости определяется двумя координатами:
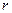 – расстояние от точки М до полюса,
– расстояние от точки М до полюса, 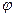 – угол между полярной осью и отрезком ОМ.
– угол между полярной осью и отрезком ОМ.
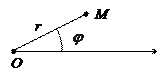 |
Для полярных координат, при выполнении контрольной работы, следует принять следующие интервалы: 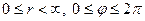
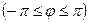 .
.
3) Связь между декартовыми и полярными координатами.
| |||
 | |||
II. Прямая линия на плоскости
4) Прямая линия на плоскости может быть задана следующими уравнениями:
а) 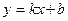 – уравнение прямой с угловым коэффициентом
– уравнение прямой с угловым коэффициентом 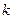 .
.
б) 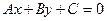 – общее уравнение прямой.
– общее уравнение прямой.
в) уравнение прямой, проходящей через заданную точку 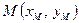 с угловым коэффициентом
с угловым коэффициентом 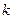 ;
; 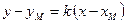 .
.
г) уравнение прямой, проходящей через две заданные точки 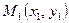 ,
, 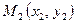
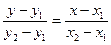 .
.
5) Условия параллельности двух прямых 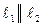 :
:
а) 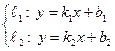
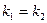 б)
б) 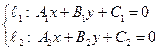
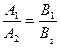 .
.
6) Условия перпендикулярности двух прямых 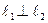 :
:
а) 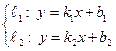
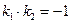 б)
б) 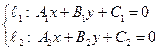
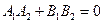 .
.
III. Теория определителей
1) Матрицей размерности 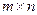 называется прямоугольная таблица чисел, состоящая из «m» строк и «n» столбцов.
называется прямоугольная таблица чисел, состоящая из «m» строк и «n» столбцов.
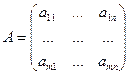 . Если
. Если 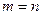 , то матрица называется квадратной.
, то матрица называется квадратной.
2) Каждой квадратной матрице можно поставить в соответствие число, которое называется определителем матрицы (обозначается 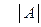 или
или 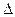 ).
).
2.1) Определители второго порядка
Матрица 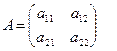 . Ее определитель вычисляется так:
. Ее определитель вычисляется так: 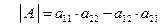 .
.
2.2)Определители третьего порядка.
Матрица 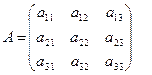 . Ее определитель
. Ее определитель 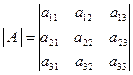 .
.
Минором 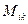 называется определитель второго порядка, который получается вычеркиванием из определителя
называется определитель второго порядка, который получается вычеркиванием из определителя 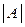 i -ой строки и k -ого столбца. Алгебраическое дополнение
i -ой строки и k -ого столбца. Алгебраическое дополнение 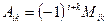 . Определитель третьего порядка вычисляется как сумма произведений элементов любой строки (любого столбца) на их алгебраические дополнения (разложением по строке или столбцу).
. Определитель третьего порядка вычисляется как сумма произведений элементов любой строки (любого столбца) на их алгебраические дополнения (разложением по строке или столбцу).
Вычислим определитель разложением по первой строке.
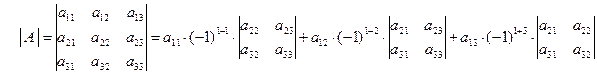 .
.
3) Решение системы линейных алгебраических уравнений. Правило Крамера.
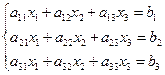
Вычисляем четыре определителя.
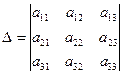 – главный определитель системы и три вспомогательных
– главный определитель системы и три вспомогательных 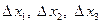 , которые получаются из главного заменой столбца при соответствующем неизвестном столбцом свободных членов
, которые получаются из главного заменой столбца при соответствующем неизвестном столбцом свободных членов 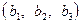 .
.
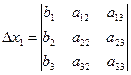 ,
, 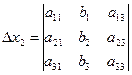 ,
, 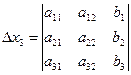 .
.
Правило Крамера:
а) Если 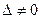 , то система имеет единственное решение
, то система имеет единственное решение 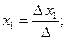
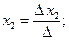
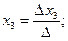
б) Если 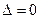 , но хотя бы один из вспомогательных не равен нулю, то система не имеет решений.
, но хотя бы один из вспомогательных не равен нулю, то система не имеет решений.
в) Если 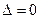 и все определители
и все определители 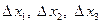 равны 0, то система имеет бесконечно много решений.
равны 0, то система имеет бесконечно много решений.
IV. Элементы векторной алгебры
1) Вектор – направленный отрезок, имеет две характеристики – длину и направление. Координаты вектора в декартовой системе координат – его проекции на оси координат.
|
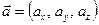 или
или  , где
, где  – векторы единичной длины, направленные по осям координат (орты).
– векторы единичной длины, направленные по осям координат (орты).
 |
| |||
Основные свойства:
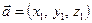 ,
, 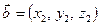
1. 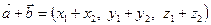 ; 2.
; 2. 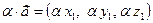 ,
, 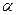 – число.
– число.
Длина вектора 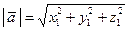 .
.
2) Скалярное произведение 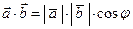 , где
, где 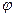 – угол между векторами.
– угол между векторами. 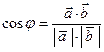 . Если
. Если 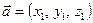 ,
, 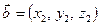 , то
, то 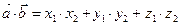 .
.
Условие перпендикулярности векторов 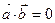
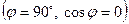 .
. 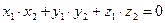
3)
|
|



 Векторное произведение
Векторное произведение  . Вектор
. Вектор  удовлетворяет трем условиям:
удовлетворяет трем условиям:
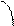 1.
1. 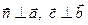
|
 2.
2.  – площадь параллелограмма, построенного на векторах
– площадь параллелограмма, построенного на векторах  и
и  .
.
 3. Вектор
3. Вектор  направлен так, что кратчайшее движение от
направлен так, что кратчайшее движение от  к
к  против часовой стрелки, если смотреть из конца вектора
против часовой стрелки, если смотреть из конца вектора 
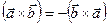 .
.
Пусть вектор 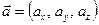 ,
, 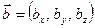 , тогда
, тогда 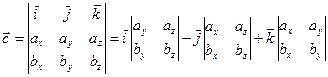
 2015-04-08
2015-04-08 447
447

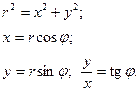
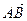 , где точка
, где точка 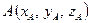 начало вектора, а точка
начало вектора, а точка 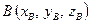 конец вектора определяются по формуле
конец вектора определяются по формуле