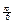2015-04-08
255
- Даны две точки:
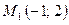в декартовой системе координат, 
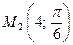– в полярной системе координат.
 |
|
| |||||
|
|
|
 | |||
 | |||
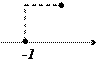Полярные координаты т.  :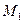
 ; 
 ;  ;
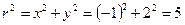
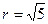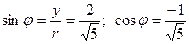
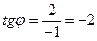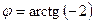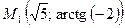
| Декартовы координаты т.  :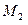
 ; 
|
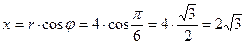
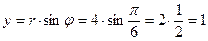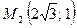
- Линия задана уравнением
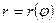. Для того, чтобы построить график рекомендуется составить таблицу значений 
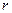для угла 
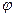, значения через промежуток 
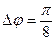, отложить полученные точки 
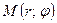на плоскости и соединить их плавной линией (подробно построение графиков рассмотрено в методическом пособии стр. 5-6). - Дано уравнение прямой
.
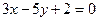1) уравнение этой прямой можно привести к уравнению с угловым коэффициентом: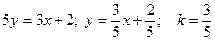 
, 
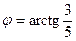– угол наклона прямой к оси ОХ.
2) Написать уравнение прямой, проходящей через точку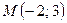 
и а) параллельной данной прямой, б) перпендикулярной данной прямой.
Уравнение прямой через точку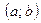 
;
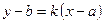Условие параллельности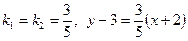 
;
Условие перпендикулярности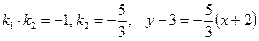 
;
3) Уравнение прямой, проходящей через точку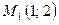 
и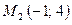 
.
; 
; 
.
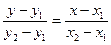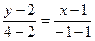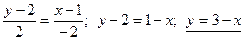4) Для решения системы уравнений по правилу Крамера необходимо вычислять определители. Рассмотрим на примере правило вычисления определителя разложением по строке или столбцу.
|
|
|
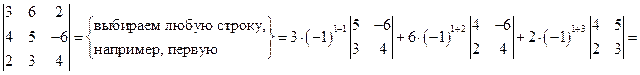
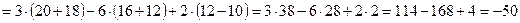
5) Даны два вектора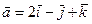 
, 
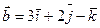. Найти площадь параллелограмма, построенного на этих векторах 
.
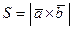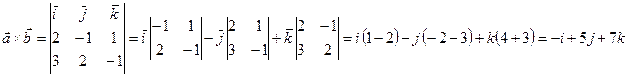
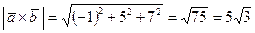кв.ед.
