Теоремы о дифференцируемых функциях

Волгодонский инженерно-технический институт - филиал НИЯУ МИФИ

КУРС ЛЕКЦИЙ

По дисциплине «Математика» 2 семестр

Для студентов заочной формы обучения

Раздел №1 «Приложения производной»

Волгодонск

Теоремы о дифференцируемых функциях.

Теорема Ферма.

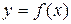Пусть функция определена и дифференцируема

на интервале (a;b) и в некоторой точке x₀ этого интервала принимает наибольшее или наименьшее значение. Тогда .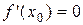

Доказательство:

По определению производной:

.

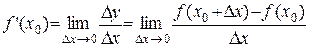Пусть для определенности в точке 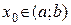функция 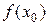принимает набольшее значение. Тогда числитель .

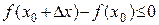Рассмотрим два случая:

1) .

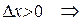
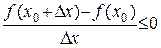По теореме о предельном переходе в неравенствах: предел дроби меньше нуля Þ .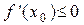

2) .

.

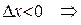
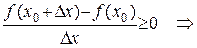
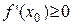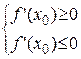
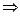
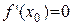Ч.т.д.

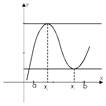
Геометрический смысл теоремы Ферма:

Так как 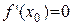, то угловой коэффициент касательной равен нулю 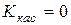Þ касательная параллельна оси ОХ.