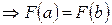Пусть функция 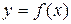 определена и непрерывна на отрезке [a;b] и дифференцируема на интервале (a;b), причем на концах интервала принимает одинаковые значения
определена и непрерывна на отрезке [a;b] и дифференцируема на интервале (a;b), причем на концах интервала принимает одинаковые значения 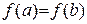 . Тогда существует точка сÎ(a;b), значения производной в которой равно 0, т.е.
. Тогда существует точка сÎ(a;b), значения производной в которой равно 0, т.е. 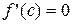 .
.
Доказательство:
 Т.к. функция
Т.к. функция 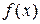 непрерывна на отрезке [a;b], то по II-й т. Вейерштрасса о непрерывных функциях
непрерывна на отрезке [a;b], то по II-й т. Вейерштрасса о непрерывных функциях 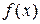 принимает на [a;b] наибольшее М и наименьшее m значения. y
принимает на [a;b] наибольшее М и наименьшее m значения. y
Возможны два случая:
1) М=m.
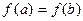
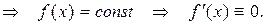
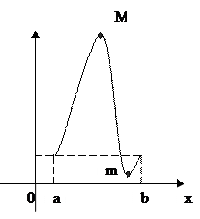 2) М
2) М 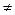 m.
m.
y
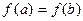
Хотя бы одна из точек, в которых функция принимает наибольшее или наименьшее значения, находится внутри [a;b].
 В этом случае в указанной точке выполняются условия теоремы Ферма и, следовательно, существует точка c, принадлежащая (a;b), в которой производная
В этом случае в указанной точке выполняются условия теоремы Ферма и, следовательно, существует точка c, принадлежащая (a;b), в которой производная 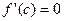 .
.
Ч.т.д.
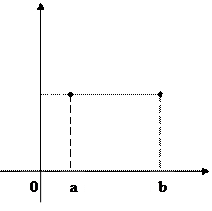
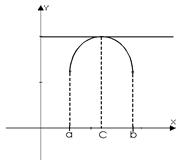
Геометрический смысл теоремы Ролля:
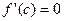 Þ Ккас=0 Þ касательная
Þ Ккас=0 Þ касательная
в точке c параллельна оси ОX.
Теорема Лагранжа.
Пусть функция 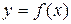 определена и непрерывна на отрезке [a;b] и дифференцируема на интервале (a;b). Тогда существует точка cÎ(a;b), значение производной в которой равно
определена и непрерывна на отрезке [a;b] и дифференцируема на интервале (a;b). Тогда существует точка cÎ(a;b), значение производной в которой равно 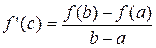 .
.
Доказательство:
Введем вспомогательную функцию 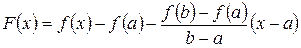 .
.
Эта функция непрерывна и дифференцируема как сумма непрерывных и дифференцируемых функций.
|


|
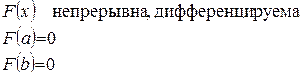
Þ существует точка сÎ(a;b) такая, что 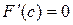 .
.
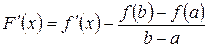 .
.
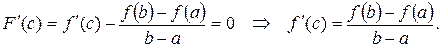
Ч.т.д.
Геометрический смысл теоремы Лагранжа:
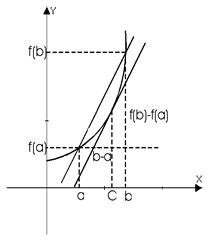
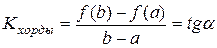 .
.
Существует точка cÎ(a;b), в которой угловой коэффициент касательной равен угловому коэффициенту хорды, соединяющей граничные точки:
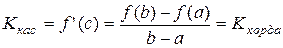 .
.
Найдется такая точка на графике, касательная в которой параллельна хорде, стягивающей концы отрезка [a;b].
Теорема Коши.
Пусть функции f(x) и g(x) определены и непрерывны на отрезке [a;b] и дифференцируемы на интервале (a;b), причем производная функции g(x) отлична от нуля, g¢(x)¹0. Тогда существует такая точка cÎ(a;b), для которой выполняется равенство: 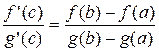 .
.
Доказательство:
Рассмотрим вспомогательную функцию:
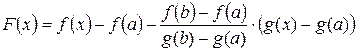 .
.
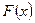 непрерывна и дифференцируема как сумма непрерывных и дифференцируемых функций.
непрерывна и дифференцируема как сумма непрерывных и дифференцируемых функций.


|
|
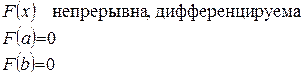
Þ существует точка сÎ(a;b): 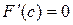 .
.
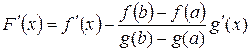 ;
; 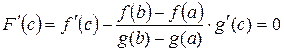 .
.
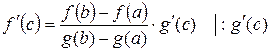 .
.
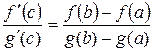 .
.
Ч.т.д.
 2015-04-12
2015-04-12 508
508