Пример 2. Через точку М(3, 5) провести прямую так, чтобы она отсекала от координатного угла равнобедренный треугольник

Через точку М(3, 5) провести прямую так, чтобы она отсекала от координатного угла равнобедренный треугольник.

«Провести прямую» - это значит записать уравнение прямой, при этом делать чертеж и проводить прямую не обязательно.

Будем искать уравнение прямой в отрезках, т. е. в форме 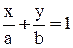, где a и b – величины отрезков, отсекаемых прямой на осях координат. По условию задачи 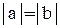и прямая проходит через точку М(3, 5). Следовательно, 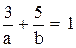. Для определения а и b имеем две системы: 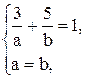и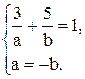

Решение первой системы: 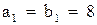, решение второй системы: 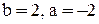. Получаем две прямые: 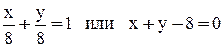и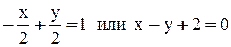

Контрольные варианты к задаче 2

1. Вершина квадрата 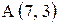, сторона СD лежит на прямой, отсекающей на осях координат отрезки 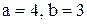. Написать уравнение стороны АД (Квадрат АВСD).

2. В треугольнике АВС даны уравнения: высоты ,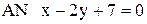

высоты 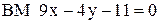и стороны 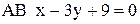. Составить уравнение третьей высоты.

3. Найти точку, симметричную точке 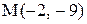относительно прямой .

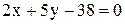4. Составить уравнение прямой, проходящей через точку пересечения прямых

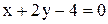и 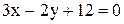и образующей угол в 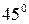с прямой .

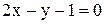5. Через точку пересечения прямых 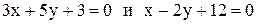провести прямую перпендикулярно прямой .

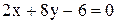6. В треугольнике АВС даны уравнения: стороны АВ 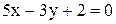и высот 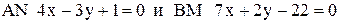. Составить уравнения двух других сторон треугольника.

7. Вычислить координаты вершин ромба, если известны уравнения двух его сторон (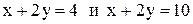) и уравнение одной из его диагоналей .

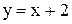8. Из точки 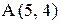выходит луч света под углом 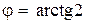к оси Ох и от нее отражается. Написать уравнения падающего и отраженного лучей.

9. Под каким углом к оси Ох наклонена прямая, проходящая через точки .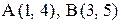

10. В квадрате АВСD даны вершина 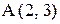и точка 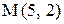- точка пересечения диагоналей. Найти уравнения сторон квадрата, не проходящих через верши-

ну А.

11. Даны точки 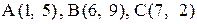. Отрезок АС разделен точкой D в отношении 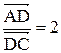. Найти расстояние от точки А до прямой ВD.

12. Отрезок прямой 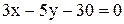, заключенный между осями координат, является диагональю квадрата. Найти уравнение одной (любой) стороны квадрата.

13. Через точку пересечения прямых 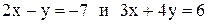провести прямую перпендикулярно прямой .

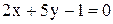14. Даны уравнения двух сторон параллелограмма: 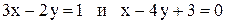и точка пересечения диагоналей 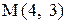. Составить уравнения двух других сторон

параллелограмма.

15. Составить уравнения прямых, проходящих через точку 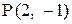и составляющих угол 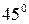с прямой .

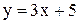16. Даны уравнения двух сторон параллелограмма 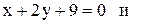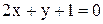- и точка пересечения его диагоналей 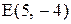. Составить уравнения

двух других его сторон.

17. Даны середины противоположных сторон квадрата 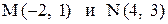. Написать уравнения двух сторон квадрата, на которых лежат точки .

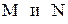18. Провести прямую так, чтобы точка 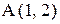была серединой ее отрезка, заключенного между осями координат. Составить уравнение этой прямой.

19. Даны две точки: 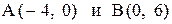. Через середину отрезка АВ провести прямую, отсекающую от оси Ох отрезок, вдвое больший, чем отрезок на оси Оу.

20. В треугольнике АВС даны вершины: 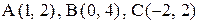. Определить: а) угол между стороной АВ и медианой стороны ВС; б) длину высоты, опущенной из вершины С.

21. Составить уравнения катетов прямоугольного равнобедренного треугольни-

ка, зная уравнение гипотенузы 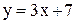и вершину прямого угла .

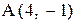22. Составить уравнение прямой, проходящей через точку 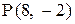и отсекающей от координатного угла треугольник площадью 8 дм².

23. В треугольнике АВС даны вершины: 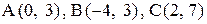. Найти точку, симметричную точке В относительно стороны АС.

24. В треугольнике АВС даны вершины: 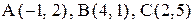. Найти угол между медианой АМ и высотой ВН.

25. Даны точки 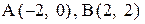. На отрезке ОА (О – начало координат), построить параллелограмм ОАСД, диагонали которого пересекаются в точке В. Написать уравнения сторон и диагоналей параллелограмма.

26. Под каким углом к оси Ох наклонена прямая, проходящая через точки ?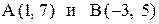

27.Составить уравнение прямой, проходящей через точку пересечения прямых 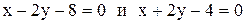и образующую с осью Ох угол, вдвое больший угла, образованного с той же осью прямой .

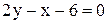28. Найти точку, симметричную точке 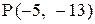относительно прямой .

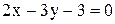29. Прямая 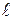отсекает на осях координат отрезки 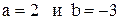. Найти точку, симметричную точке 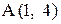относительно прямой .

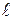30. Даны уравнения двух сторон параллелограмма: 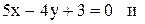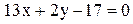- и одна из его вершин 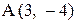. Найти точку пересечения его диагоналей.