2015-04-12
445
Найти наибольшее и наименьшее значения функции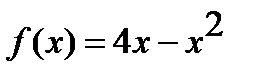 
на отрезке 
.
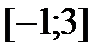Решение. Определяем критические, или стационарные, точки функции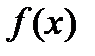 
:
; 
; 
; 
.
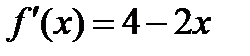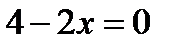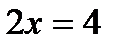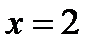Рассматриваем только те стационарные точки, которые принадлежат отрезку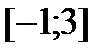 
. Такой точкой является точка 
.
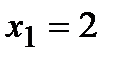Вычисляем значения функции на концах промежутка и в точке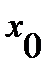 
:
1) 
;
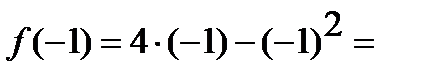
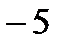2) 
= 
;
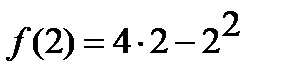3) 
= 
.
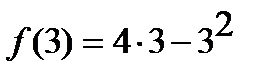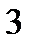Ясно, что наибольшее значение функции будет равно 
, которое она принимает в точке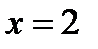 
; наименьшее значение принимается функцией в точке 
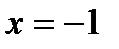и равно 
.
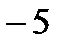Общее исследование функций и построение их графиков удобно выполнять по следующей схеме:
1) Найти область определения функции.
2) Найти точки пересечения с осями координат.
3) Выяснить, не является ли функция четной или нечетной, периодической или непериодической.
4) Найти точки экстремума функции, вычислить значения функции в этих точках. Установить интервалы монотонности функции.
5) Найти точки перегиба графика функции, вычислить значения функции в этих точках. Установить интервалы выпуклости и вогнутости графика функции.
6) Найти асимптоты графика функции.
7) Используя результаты исследований, построить график функции.
Пример. Исследовать функцию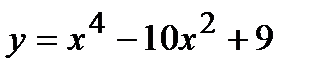 
и построить ее график.
