Функция 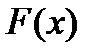 называется первообразной функции
называется первообразной функции 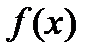 на некотором интервале
на некотором интервале 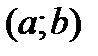 , если
, если 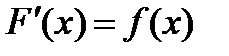 для всех значений
для всех значений 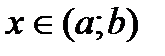 . Если
. Если 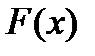 — первообразная
— первообразная 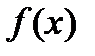 , то очевидно, что бесконечное множество всех первообразных
, то очевидно, что бесконечное множество всех первообразных 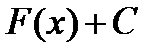 , отличающихся только константой, также будет первообразной
, отличающихся только константой, также будет первообразной 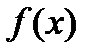 . Множество всех первообразных функций
. Множество всех первообразных функций 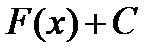
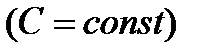 называется неопределенным интегралом от функции
называется неопределенным интегралом от функции 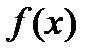 и обозначается
и обозначается 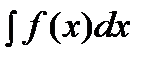 . При этом
. При этом 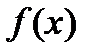 называется подынтегральной функцией,
называется подынтегральной функцией, 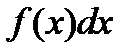 — подынтегральным выражением,
— подынтегральным выражением, 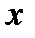 — переменной интегрирования.
— переменной интегрирования.
Согласно вышеприведенному:
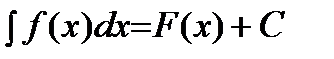 ,
,
где 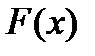 — некоторая первообразная функции
— некоторая первообразная функции 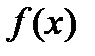 ;
; 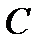 — произвольная постоянная.
— произвольная постоянная.
Неопределенный интеграл обладает следующими свойствами:
1) 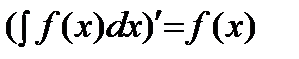 .
.
2) 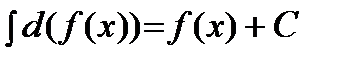 .
.
3) 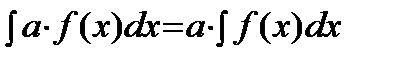 , где
, где 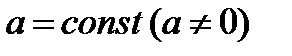 .
.
4) 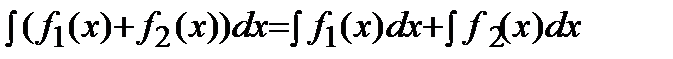 .
.
5) 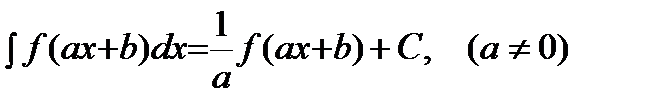 .
.
Таблица основных неопределенных интегралов:
1) 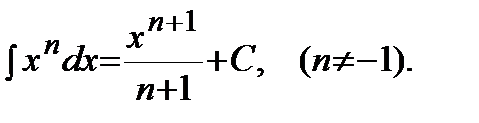
| 2) 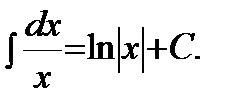
|
3) 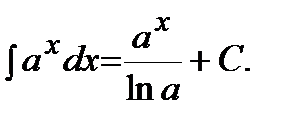
| 4) 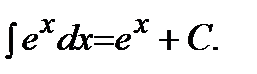
|
5) 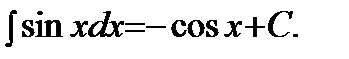
| 6) 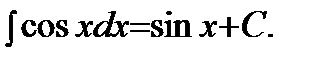
|
7) 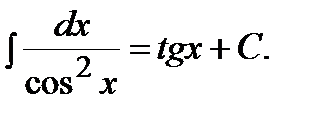
| 8) 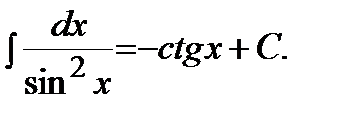
|
9) 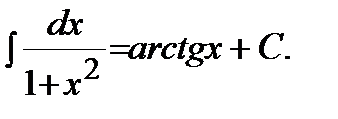
| 10) 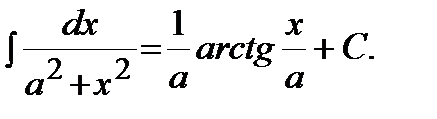
|
11) 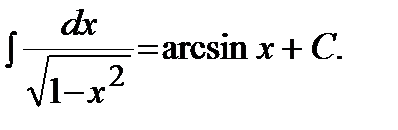
| 12) 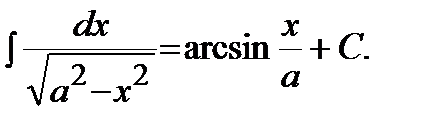
|
13) 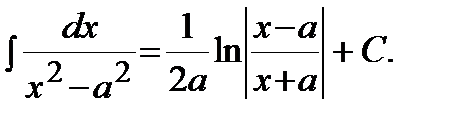
| 14) 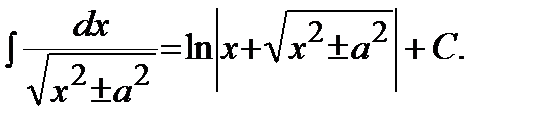
|
 2015-04-12
2015-04-12 366
366








