1. 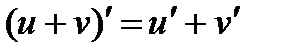 2.
2. 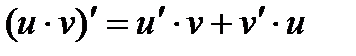 , в частности,
, в частности, 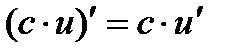 3.
3. 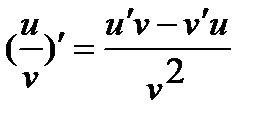 , где
, где 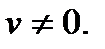
Задача. Найти производные следующих функций:
а) 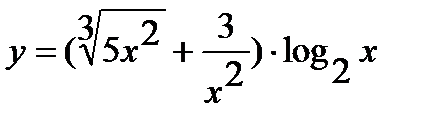 ; б)
; б) 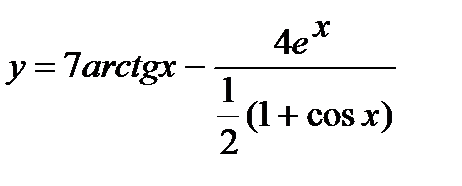 .
.
Решение. а) Преобразуем выражение в скобках, переходя к дробным и отрицательным показателям. Получим
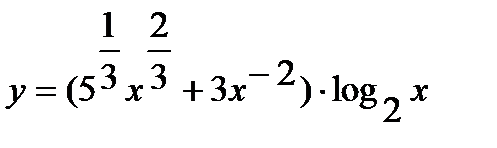 .
.
Используя правило дифференцирования произведения и суммы находим 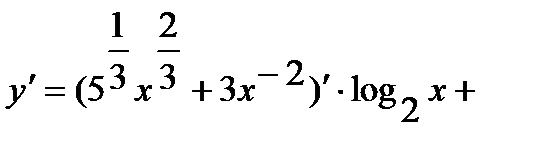
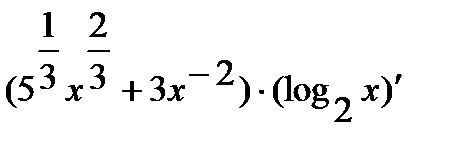 =
=
= 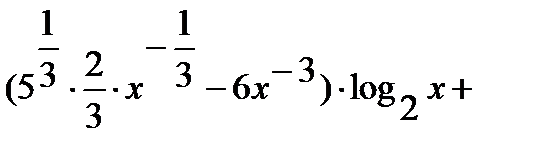
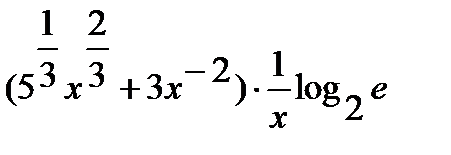 .
.
б) Проведем предварительное преобразование функции:
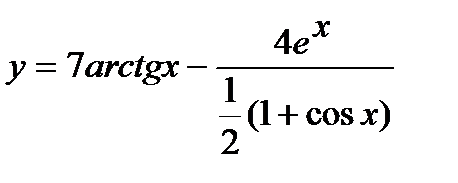 =
= 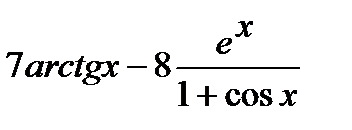 .
.
Используя правила дифференцирования произведения, суммы и частного, получим
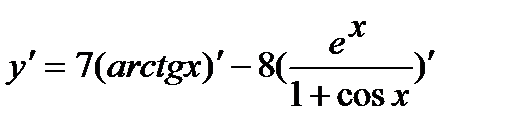 =
=
= 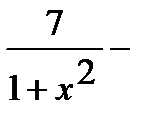
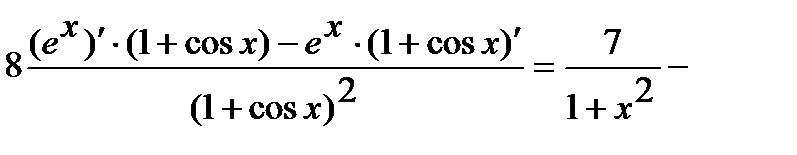
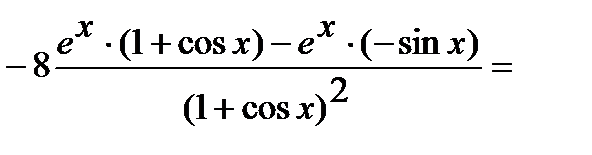
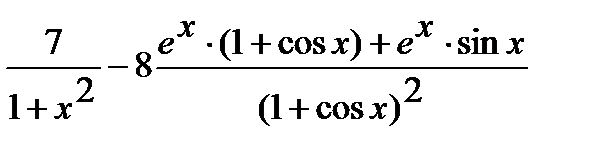 .
.
Дифференцирование сложной функции
Если функция 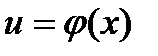 дифференцируема в точке
дифференцируема в точке 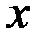 , а функция
, а функция 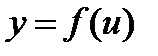 дифференцируема в точке
дифференцируема в точке 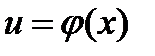 , то сложная функция
, то сложная функция 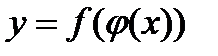 дифференцируема в точке
дифференцируема в точке 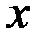 и
и
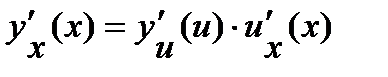 ,
,
где индекс внизу показывает, по какой переменной берется производная.
Задача. Найти производные следующих функций:
а) 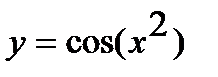 ; г)
; г) 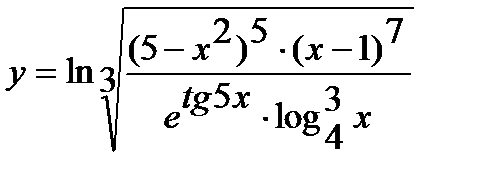 ;
;
б) 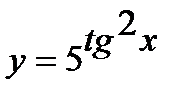 ;
;
в) 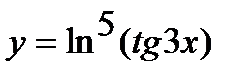 ;
;
Решение. а) Функцию 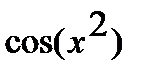 представим как композицию функций
представим как композицию функций 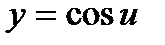 и
и 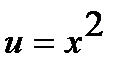 . Используя таблицу производных, находим:
. Используя таблицу производных, находим: 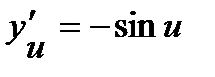 ,
, 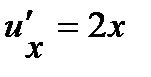 .
.
Тогда
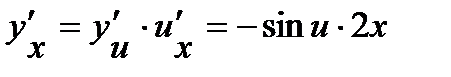
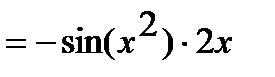 .
.
б) Функцию 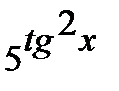 представим как композицию функций
представим как композицию функций 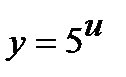 ,
,
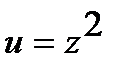 и
и 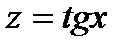 .Найдем производные по промежуточным аргументам:
.Найдем производные по промежуточным аргументам: 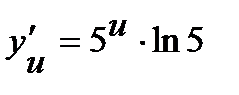 ,
, 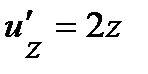 и
и 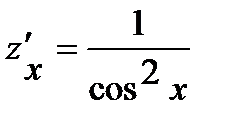 .
.
Производную сложной функции находим по формуле 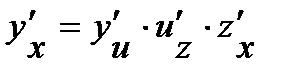 . Окончательно получим
. Окончательно получим 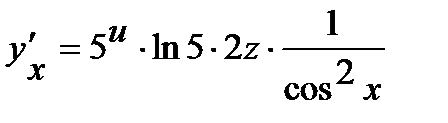 =
= 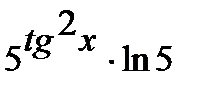
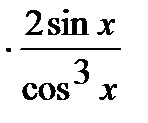 .
.
Аналогично решается задача в:
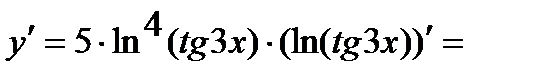
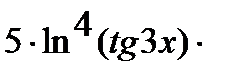
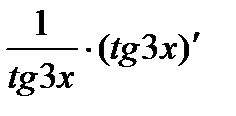 =
=
= 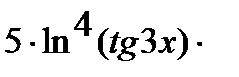
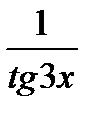

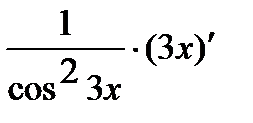 =
= 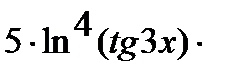
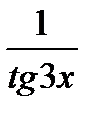
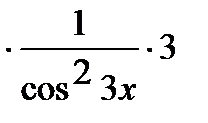 .
.
г) Предварительно упростив выражение, определяющее функцию, до вида
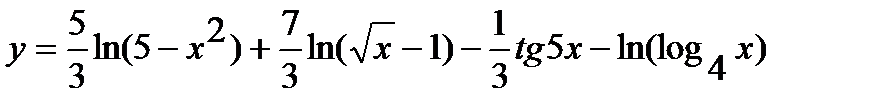 ,
,
находим производную:
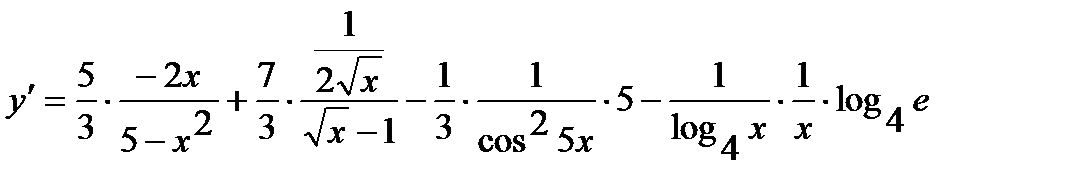 .
.
 2015-04-12
2015-04-12 403
403








