Решение. 1) Функция определена и непрерывна на всей оси

1) Функция определена и непрерывна на всей оси. Итак, .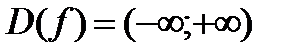

2) Найдем точки пересечения с осями координат.

а) с осью ОХ: , .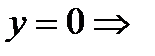

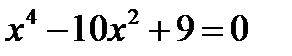
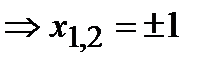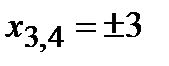Следовательно, точки пересечения с осью ОХ - , , , ;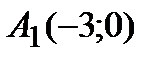

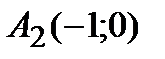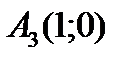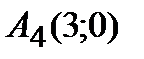б) с осью ОY: .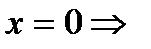

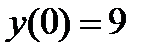Следовательно, точка пересечения с осью ОY - .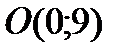

3) Функция четная, так как 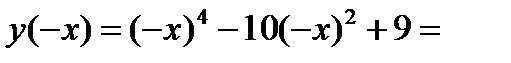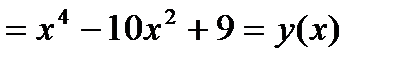(поэтому ее график будет симметричен относительно оси OY).

Функция непериодическая.

4) С помощью первой производной найдем промежутки возрастания и убывания функции.

Имеем 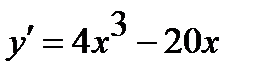=0. Следовательно, точки 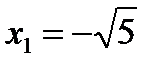, , 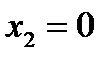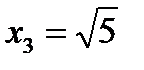будут подозрительными на экстремум. Разбиваем всю область определения на промежутки 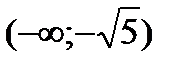, , 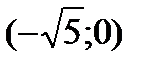, 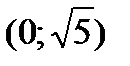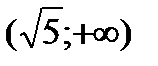и исследуем функцию для 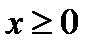. Информация о поведении функции на интервале 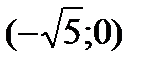необходима для анализа функции в точке 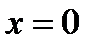. По знаку производной определяем монотонность функции на каждом промежутке. Результаты исследований заносим в таблицу:

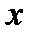
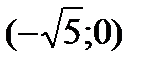
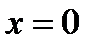
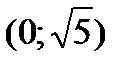
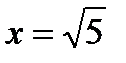
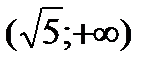
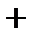
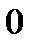
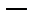
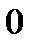
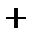
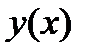
	Возрастает		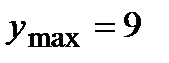Убывает		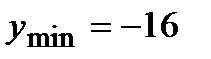Возрастает

5) Чтобы исследовать функцию на выпуклость, найдем вторую производную: 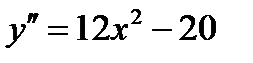. Находим точки, в которых 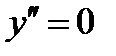или 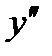не существует.

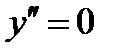при .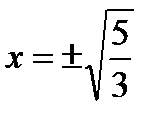

Исследуем знак второй производной на промежутках 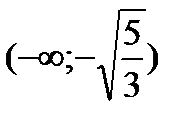, , 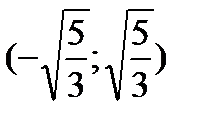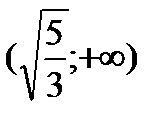и результаты исследований представим в таблице:

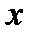
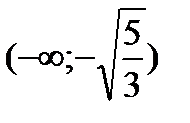
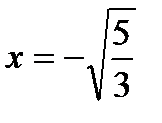
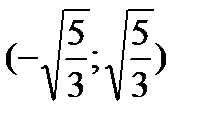
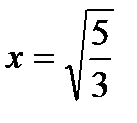
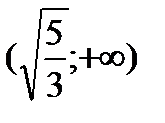
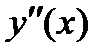
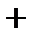
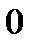
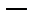
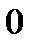
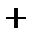
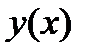
	Выпукла	Перегиб	Вогнута	Перегиб	Выпукла

6) Вертикальных асимптот нет, поскольку область определения функции – вся числовая ось.

Найдем наклонную асимптоту :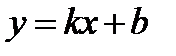

= .

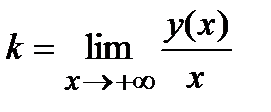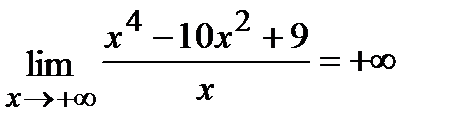Следовательно, наклонных асимптот нет.

7) На основе проведенного исследования функции строим ее график (рис.1).

Рис. 1

Пример. Исследовать функцию 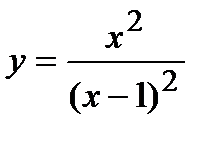и построить ее график.