Рассмотрим две плоскости, заданные общими уравнениями
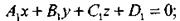
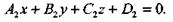
Предположим, что условие
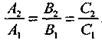
для этих плоскостей не выполнено.
Пусть
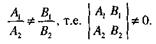
В этом случае плоскости пересекаются по прямой, определяемой уравнениями
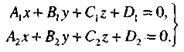
Эти уравнения приведем к параметрическому виду, для чего нужно выбрать точку этой прямой и направляющий вектор. В качестве последнего можно взять вектор 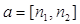 , где
, где 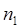 и
и 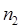 - нормальные векторы рассматриваемых плоскостей. Так как
- нормальные векторы рассматриваемых плоскостей. Так как 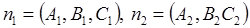 , то
, то
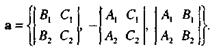
Чтобы выбрать точку, фиксируем произвольное значение 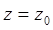 в последних уравнениях, получим систему двух уравнений
в последних уравнениях, получим систему двух уравнений
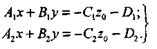
Решая эту систему (определитель ее отличен от нуля), получаем значения 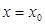 и
и 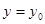 . Итак, фиксирована точка
. Итак, фиксирована точка 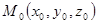 .
.
Искомые параметрические уравнения принимают вид:
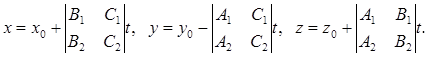
 2015-04-12
2015-04-12 399
399








