Направляющим вектором прямой называется любой вектор, лежащий на прямой или параллельный ей.
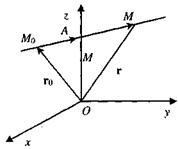
Составим уравнение прямой, проходящей через точку 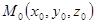 и имеющей направляющий вектор
и имеющей направляющий вектор 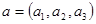 . Уравнение вида:
. Уравнение вида:
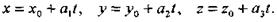
Называются параметрическими уравнениями прямой.
Каждое из последних уравнений разрешим относительно t:
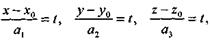
Откуда
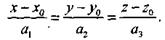
Данные уравнения называются каноническими уравнениями прямой.
Пусть даны две различные точки 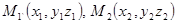 . В качестве направляющего вектора прямой можно взять вектор
. В качестве направляющего вектора прямой можно взять вектор
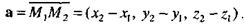
Поскольку прямая проходит через точку
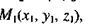
ее канонические уравнения в соответствии с каноническим уравнением запишутся так:
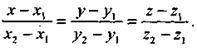
Эти уравнения являются уравнениями прямой, проходящей через две указанные точки.
Рассмотрим две прямые, заданные параметрическими уравнениями
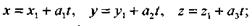
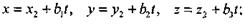
первая из этих прямых проходит через точку 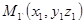 , вторая через точку
, вторая через точку 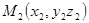 , прямые имеют соответственно направляющие векторы
, прямые имеют соответственно направляющие векторы
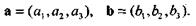
Поскольку угол между прямыми равен углу между их направляющими векторами, то
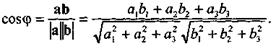
Очевидно, условие перпендикулярности прямых выражается равенством
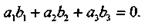
Необходимое и достаточное условие параллельности прямых выражается равенствами
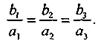
Исследуем вопрос о взаимном расположении двух прямых в пространстве. Кроме векторов a и b рассмотрим еще вектор М 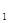 М2 = (х2 - х1, у2 - у1,z
М2 = (х2 - х1, у2 - у1,z 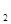 - z
- z 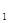 ).
).
Очевидно, данные прямые являются скрещивающимися тогда и только тогда, когда векторы a b и М 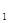 М2 некомпланарны, в этом случае их смешанное произведение отлично от нуля, т.е. [а, b ] М1М2
М2 некомпланарны, в этом случае их смешанное произведение отлично от нуля, т.е. [а, b ] М1М2 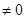 , или
, или
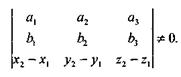
Данные прямые лежат в одной плоскости тогда и только тогда, когда векторы [а, b ], М1М2 компланарны, а в этом случае [а, b ] М1М2 =0, или
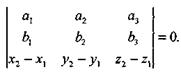
 2015-04-12
2015-04-12 2797
2797
