Пример 2. Вычислить определитель четвертого порядка

Вычислить определитель четвертого порядка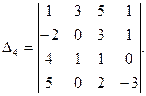

Решение.

• Вычислим определитель, разложив его по элементам второго столбца

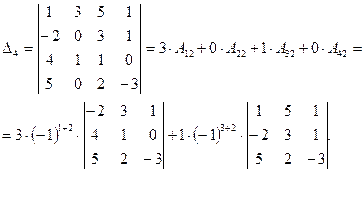
• Подсчитаем определители третьего порядка отдельно:

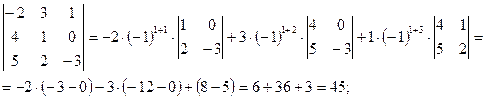
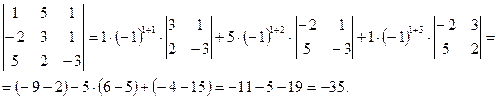
• Таким образом, определитель четвертого порядка будет равен:

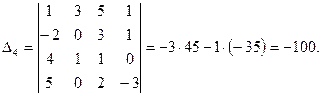
· Вычислим определитель четвертого порядка, используя свойства определителя. Для этого получим нули во втором столбце: умножим третью строку на (-3) и сложим ее с первой. Полученный в результате этого определитель вычислим, разложив его по элементам второго столбца.

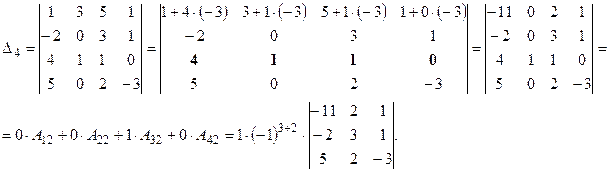
· Подсчитаем определитель третьего порядка отдельно. Используя свойства определителей, получим нули в первой строке. Для этого третий столбец умножим на (-2) и сложим его со вторым столбцом; умножим третий столбец на 11 и прибавим его к первому столбцу:

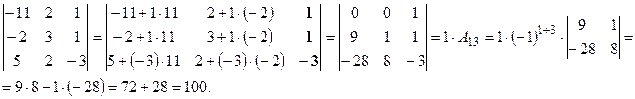
• Таким образом, определитель четвертого порядка будет равен

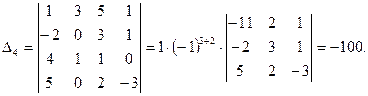
Ответ: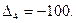

Замечание. Выбор способа вычисления определителя (выбор строки или столбца при разложении, применение свойств определителей) не влияет на его значение.

Пример 3. Решить методом Гаусса систему линейных алгебраических уравнений:

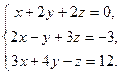
Решение.

• Запишем систему в виде расширенной матрицы, т.е. составим матрицу из коэффициентов системы и присоединим к ней столбец свободных элементов, для удобства отделенный вертикальной чертой:

.

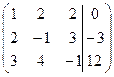• Выполняя элементарные преобразования над строками этой расширенной матрицы, приведем ее к треугольному виду. Для этого к элементам второй строки добавим соответствующие элементы первой строки, умноженные на (-2); к элементам третьей строки добавим соответствующие элементы первой строки, умноженные на (-3). Элементы первой строки оставляем без изменений.

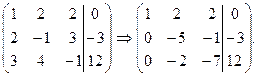
• Полученную матрицу преобразуем таким образом, чтобы в третьей строке до черты оставался один элемент, не равный нулю. Для этого к элементам третьей строки добавим соответствующие элементы второй строки, умноженные на 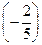. Элементы первой и второй строк оставляем без изменений.

.

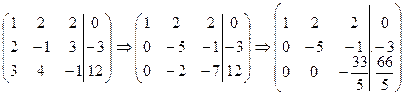• От расширенной матрицы перейдем к системе уравнений, эквивалентной заданной
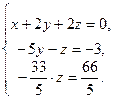
• Решая третье уравнение системы, найдем значение : .
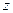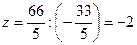• Подставляя значение 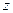= - 2 во втрое уравнение системы, получим .
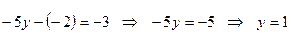• Подставив в первое уравнение 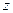= - 2, 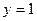, получим значение х:

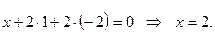
• Проверка

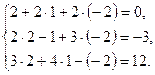
Ответ: .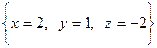

Пример 4. Решить методом Гаусса систему линейных алгебраических уравнений:

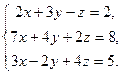
Решение.

• Запишем систему в виде расширенной матрицы, т.е. составим матрицу из коэффициентов системы и присоединим к ней столбец свободных элементов, для удобства отделенный вертикальной чертой:

.

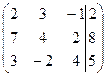• Третий столбец сделаем первым: .
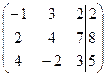• Выполняя элементарные преобразования над строками этой расширенной матрицы, приведем ее к треугольному виду. Для этого к элементам второй строки добавим соответствующие элементы первой строки, умноженные на 2; к элементам третьей строки добавим соответствующие элементы первой строки, умноженные на 4. Элементы первой строки оставляем без изменений.

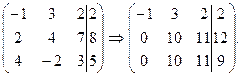
• Полученной матрице преобразуем таким образом, чтобы в третьей строке до черты оставался один элемент, не равный нулю. Для этого к элементам третьей строки добавим соответствующие элементы второй строки, умноженные на 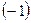. Элементы первой и второй строк оставляем без изменений.

.

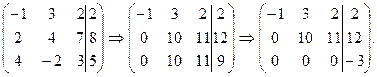• От расширенной матрицы перейдем к системе уравнений, эквивалентной заданной
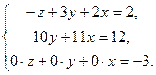
• Полученная система несовместна, так как ее последнее уравнение не имеет смысла. Следовательно, исходная система также несовместна.

Ответ: система несовместна.

.