ПРАКТИЧЕСКАЯ РАБОТА по теме "МЕЖОТРАСЛЕВОЙ БАЛАНС"
Цель балансового метода - ответить на вопрос, рассматриваемый в макроэкономике и связанный с эффективностью ведения многоотраслевого хозяйства: каким должен быть объем производства каждой из п отраслей, чтобы удовлетворять все потребности в продукции этой отрасли? При этом каждая отрасль выступает, с одной стороны, как производитель некоторой продукции, а с другой - как потребитель продукции и своей, и произведенной другими отраслями. Модель межотраслевого баланса (МОБ) одна из самых простых экономико-математических моделей. Связь между отраслями, как правило, отображается в балансовых таблицах, содержащих данные о производстве и потреблении продукции различных отраслей или предприятий. Математическая модель, позволяющая их анализировать, разработана в 1936г. В.Леонтьевым [Леонтьев Василий (1906-1999) - американский экономист]. Характерные черты и особенности этого метода описывается с помощью матричных моделей баланса. Из математических методов здесь главным образом используется аппарат линейной алгебры.
Рассмотрим пример предельно упрощенной системы, состоящей из двух производственных отраслей. Пусть исполнение баланса за предшествующий период характеризуется данными, приведенными в таблице 1.
Таблица 1.
| Производящие отрасли | Потребляющие отрасли | Итого затрат 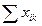 | Конечный продукт 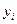 | Валовый выпуск 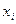 | |
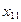 | 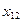 | 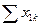 | 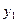 | 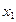 | |
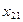 | 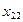 | 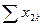 | 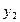 | 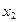 | |
| Итого затрат В k -ю отрасль | 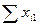 | 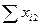 |
Введем следующие обозначения:
-
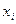 - валовый (общий) объем продукции i-ой отрасли за планируемый период;
- валовый (общий) объем продукции i-ой отрасли за планируемый период; -
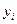 - объем конечного продукта i-ой отрасли для непроизводственного потребления;
- объем конечного продукта i-ой отрасли для непроизводственного потребления;
· 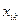 - объем продукции i-ой отрасли, потребляемый k-ой отраслью, для обеспечения выпуска ее продукции в размере
- объем продукции i-ой отрасли, потребляемый k-ой отраслью, для обеспечения выпуска ее продукции в размере 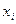 .
.
· Так как валовый объем продукции любой i-ой отрасли равен суммарному объему продукции, потребляемой п отраслями, и конечного продукта, то
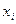 =
= 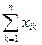 +
+ 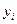 (i=1,…,n). (1)
(i=1,…,n). (1)
Уравнения (1) называются соотношениями баланса. Будем рассматривать стоимостный межотраслевой баланс, когда все величины, входящие в уравнения (1), имеют стоимостное выражение.
- Коэффициенты прямых затрат:
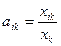 (i, k =1,…,n), (2)
(i, k =1,…,n), (2)
Показывающие затраты i-ой отрасли на производство единицы продукции k-ой отрасли.
· Найденные коэффициенты прямых затрат и образуют неотрицательную матрицу прямых затрат А= 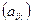 . Матрица прямых затрат должна удовлетворять критерию продуктивности: для любых i,k-1,2,…, п max
. Матрица прямых затрат должна удовлетворять критерию продуктивности: для любых i,k-1,2,…, п max 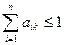 .
.
· Можно полагать, что в некотором промежутке времени коэффициенты 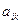 будут постоянными и зависящими от сложившейся технологии производства. Это означает линейную зависимость материальных затрат валового выпуска, т.е.
будут постоянными и зависящими от сложившейся технологии производства. Это означает линейную зависимость материальных затрат валового выпуска, т.е. 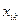 =
= 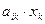 . (3)
. (3)
Вследствие чего построенная на этом основании модель межотраслевого баланса получила название линейной. Тогда соотношения баланса (1) примут вид: 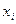 =
= 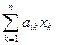 +
+ 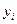 (i=1,…,n). (4)
(i=1,…,n). (4)
- Систему межотраслевого баланса (1) можно записать в матричном виде: (Е-A)Х=Y, (5)
где 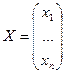 - вектор валового продукта;
- вектор валового продукта; 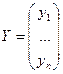 - вектор конечного продукта,
- вектор конечного продукта,
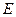 - единичная матрица, А – матрица прямых затрат.
- единичная матрица, А – матрица прямых затрат.
· Основная задача межотраслевого баланса состоит в том отыскании такого вектора валового выпуска Х, который при известной матрице прямых затрат А обеспечивает заданный вектор конечного продукту Y.
· 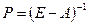 - матрица коэффициентов полных затрат. Элементы матрицы Р включают не только затраты i-ой отрасли, необходимые для создания одной единицы продукции k-ой отрасли, но и те затраты, которые необходимы для создания в каждой отрасли одной единицы конечного продукта.
- матрица коэффициентов полных затрат. Элементы матрицы Р включают не только затраты i-ой отрасли, необходимые для создания одной единицы продукции k-ой отрасли, но и те затраты, которые необходимы для создания в каждой отрасли одной единицы конечного продукта.
· Объемы производства отраслей определяются как: Х=РY.
· Чистая продукция отрасли – это разность между валовой продукцией этой отрасли и продукцией всех отраслей на производство этой отрасли.
· Косвенные затраты: С=Р-А-Е.
Задача. Три отрасли промышленности I, II и III являются производителями и в то же время потребителями некоторой продукции. Их взаимосвязи определяет матрица А коэффициентов прямых затрат и вектором конечной продукции Y:
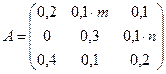 ,
, 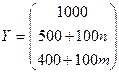 .
.
Найти коэффициенты полных затрат; плановые объемы валовой продукции 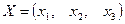 ; величину межотраслевых потоков (т.е. значения
; величину межотраслевых потоков (т.е. значения 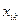 ), матрицу косвенных затрат; определить чистую продукцию каждой отрасли. Результаты расчетов оформить в виде таблицы межотраслевого баланса 1. Расчеты рекомендуется производить с точностью до трех знаков после запятой.
), матрицу косвенных затрат; определить чистую продукцию каждой отрасли. Результаты расчетов оформить в виде таблицы межотраслевого баланса 1. Расчеты рекомендуется производить с точностью до трех знаков после запятой.
Решение нулевого варианта.
Задача. Три отрасли промышленности I, II и III являются производителями и в то же время потребителями некоторой продукции. Их взаимосвязи определяет матрица А коэффициентов прямых затрат и вектором конечной продукции Y:
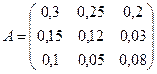 ,
, 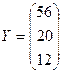 .
.
Найти коэффициенты полных затрат; плановые объемы валовой продукции 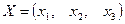 ; величину межотраслевых потоков (т.е. значения
; величину межотраслевых потоков (т.е. значения 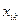 ), матрицу косвенных затрат; определить чистую продукцию каждой отрасли.
), матрицу косвенных затрат; определить чистую продукцию каждой отрасли.
Решение.
1. Найдем матрицу (Е-А): 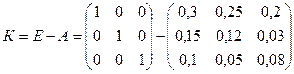 =
= 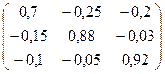 .
.
2. Для определения матрицы полных затрат найдем матрицу обратную К.
· Вычислим определитель: 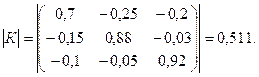
· Так как 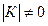 , то существует матрица
, то существует матрица 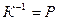 обратная заданной матрице К.
обратная заданной матрице К.
· Находим алгебраические дополнения для элементов матрицы К:
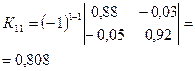 | 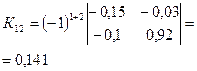 | 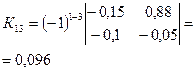 |
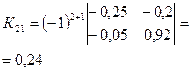 | 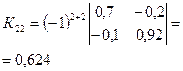 | 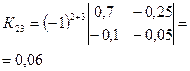 |
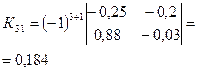 | 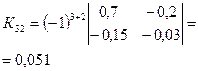 | 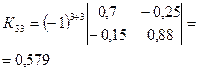 |
· Из алгебраических дополнений составляем матрицу 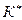 и транспонируем ее:
и транспонируем ее:
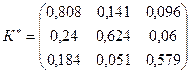 и
и 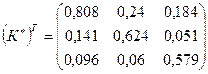 .
.
· Получаем обратную матрицу(она является матрицей полных затрат):
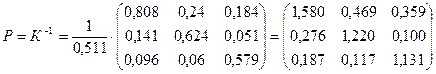 .
.
3. Находим объем производства отраслей (валовая продукция):
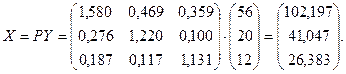
Следовательно, плановые объемы валовой продукции трех отраслей, необходимые для обеспечения заданного уровня конечной продукции равны: 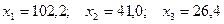 .
.
4. Для составления баланса рассчитываем межотраслевые потоки средств производства:
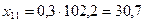 ; ; | 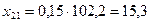 ; ; | 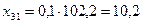 ; ; |
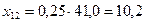 ; ; | 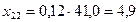 ; ; | 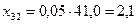 ; ; |
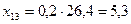 ; ; | 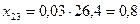 ; ; | 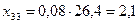 . . |
Результаты вычислений представим в форме межотраслевого баланса (таблица 2).
5. Величина чистой продукции определяется здесь как разница между валовой продукцией отрасли и суммой межотраслевых потоков в каждом столбце.
Таблица 2.
| Производящие отрасли | Потребляющие отрасли | Конечная продукция | Валовая продукция | ||
| 30,7 | 10,2 | 5,3 | 102,2 | ||
| 15,3 | 4,9 | 0,8 | 41,0 | ||
| 10,2 | 2,1 | 2,1 | 26,4 | ||
| Чистая продукция | 46,0 | 23,8 | 18,2 | - | - |
| Валовая продукция | 102,2 | 41,0 | 26,4 | - | 169,6 |
6. Найдем матрицу косвенных затрат:
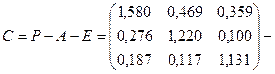
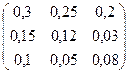
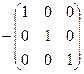 = =
= = 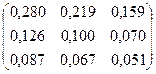 .
.
Замечание. Для того чтобы составить условие задачи для своего варианта, необходимо взять две последние цифры своего шифра (А - предпоследняя цифра, В – последняя) и выбрать из таблицы 3 параметр т, а из таблицы 4 параметр п. Эти два числа подставить в условие задачи.
Таблица 3.
| А | ||||||||||
| т |
Таблица 4.
| В | ||||||||||
| п |
 2015-04-12
2015-04-12 1470
1470







