Персептрон Розенблатта

Одной из первых искусственных сетей, способных к перцепции (восприятию) и формированию реакции на воспринятый стимул, явился PERCEPTRON Розенблатта Персептрон рассматривался его автором не как конкретное техническое вычислительное устройство, а как модель работы мозга.

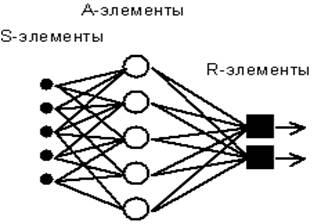
Рис. 4.1. Элементарный персептрон Розенблатта.

Простейший классический персептрон содержит нейроподобные элементы трех типов (см. Рис. 4.1), назначение которых в целом соответствует нейронам рефлекторной нейронной сети, рассмотренной в предыдущей лекции. S-элементы формируют сетчатку сенсорных клеток, принимающих двоичные сигналы от внешнего мира. Далее сигналы поступают в слой ассоциативных или A-элементов (для упрощения изображения часть связей от входных S-клеток к A-клеткам не показана). Только ассоциативные элементы, представляющие собой формальные нейроны, выполняют нелинейную обработку информации и имеют изменяемые веса связей. R-элементы с фиксированными весами формируют сигнал реакции персептрона на входной стимул.

Способность искусственных нейронных сетей обучаться является их наиболее интригующим свойством. Подобно биологическим системам, которые они моделируют, эти нейронные сети сами моделируют себя в результате попыток достичь лучшей модели поведения.

Обучение может быть с учителем или без него. Для обучения с учителем нужен «внешний» учитель, который оценивал бы поведение системы и управлял ее последующими модификациями. При обучении без учителя сеть путем самоорганизации делает требуемые изменения. Обучение персептрона является обучением с учителем.

Персептрон обучают, подавая множество образов по одному на его вход и подстраивая веса до тех пор, пока для всех образов не будет достигнут требуемый выход.

Допустим, есть следующая модель персептрона:

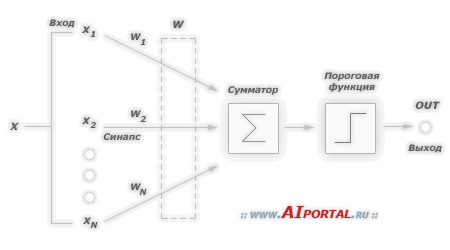
Алгоритм обучения персептрона следующий:

1. Присвоить синаптическим весам 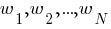некоторые начальные значения. Например, нулю.

2. Подать входной образ 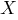и вычислить 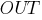. Если 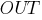правильный, то переходят к шагу 4. Иначе к шагу 3.

3. Применяя дельта-правило (см. ниже) вычислить новые значения синаптических весов.

4. Повторить шаги 2-4 данного алгоритма обучения персептрона пока сеть не станет выдавать ожидаемый выход на векторах из обучающей выборки или пока отклонение не станет ниже некоторого порога.

Т.о. образом логика обучения персептрона следующая: если сигнал персептрона при некотором образе верен, то ничего корректировать не надо, если нет – производится корректировка весов.

Правила корректировки весов следующие:

1. Если 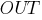неверен и равен нулю, то необходимо
увеличить веса тех входов, на которые была подана единица.

2. Если 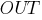неверен и равен единице, то необходимо
уменьшить веса тех входов, на которые была подана единица.

Поясним эти правила. Допустим, что на вход был подан некоторый обучающий двоичный вектор 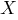. Этому вектору соответствует выход 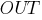равный единице. И этот выход неправильный. Тогда веса, присоединенные к единичным входам, должны быть уменьшены, так как они стремятся дать неверный результат. Аналогично, если некоторому другому обучающему вектору 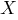соответствует неправильный выход 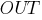равный нулю, то веса, присоединенные к единичным входам, должны быть уже уменьшены.