1) Каждый элемент можно представить как произведение этого элемента на вещественное число 1
2) Для каждого элемента существует единственный противоположный элемент
3) Нулевой элемент равен произведению произвольного элемента на вещественное число 0
4) Для каждого элемента противоположный элемент равен произведению этого элемента на вещественное число -1
7. Пусть 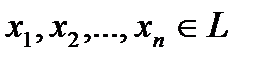 – некоторые элементы векторного пространства,
– некоторые элементы векторного пространства, 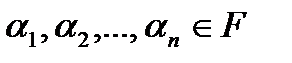 – некоторые скаляры. Выражение
– некоторые скаляры. Выражение 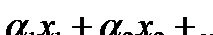 является
является
1) Линейной комбинацией 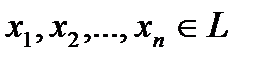 над полем
над полем 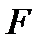
2) Определением линейной независимости элементов 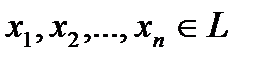 над полем
над полем 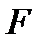
3) Определением линейной зависимости элементов 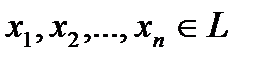 над полем
над полем 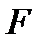
4) Определением базиса 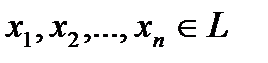
8. Пусть 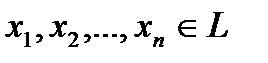 – некоторые элементы векторного пространства,
– некоторые элементы векторного пространства, 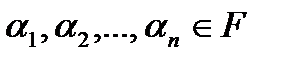 – некоторые скаляры. Выражение
– некоторые скаляры. Выражение 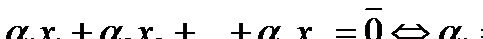 является
является
1) Линейной комбинацией 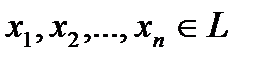 над полем
над полем 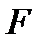
2) Определением линейной независимости элементов 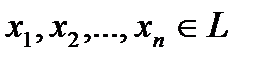 над полем
над полем 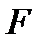
3) Определением линейной зависимости элементов 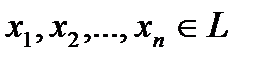 над полем
над полем 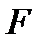
4) Определением базиса 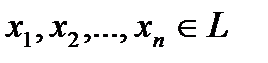
9. Пусть 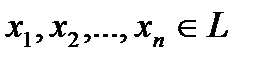 – некоторые элементы векторного пространства,
– некоторые элементы векторного пространства, 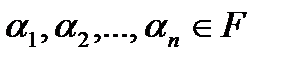 – некоторые скаляры. Выражение
– некоторые скаляры. Выражение 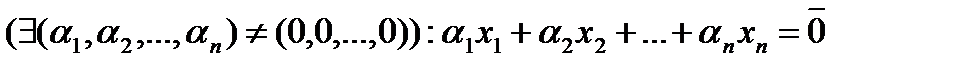 является
является
1) Линейной комбинацией 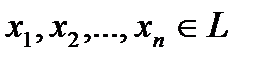 над полем
над полем 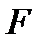
2) Определением линейной независимости элементов 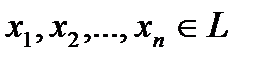 над полем
над полем 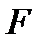
3) Определением линейной зависимости элементов 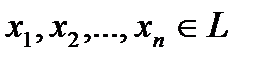 над полем
над полем 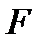
4) Определением базиса 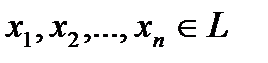
10. Пусть 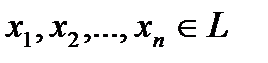 – некоторые элементы векторного пространства, образующие линейно независимую систему векторов над полем
– некоторые элементы векторного пространства, образующие линейно независимую систему векторов над полем 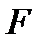 ,
, 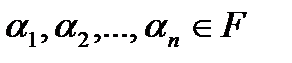 некоторые скаляры. Выражение
некоторые скаляры. Выражение  является
является
1) Линейной комбинацией 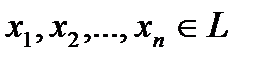 над полем
над полем 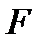
2) Определением линейной независимости элементов 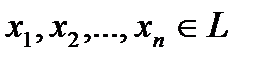 над полем
над полем 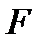
3) Определением линейной зависимости элементов 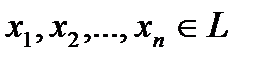 над полем
над полем 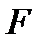
4) Определением базиса 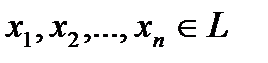
 2015-04-12
2015-04-12 214
214








