2015-04-12
382
Пример: Пусть вектор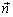 
единичной длины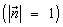 
образует с
вектором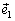 
ортонормированного
базиса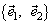 
на плоскости угол
φ, тогда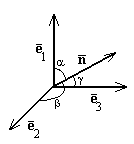 
.
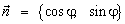
Пример: Пусть вектор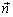
единичной длины 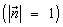образует с
векторами ,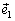 
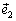
и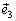 
ортонормированного базиса в
пространстве углы α, β, γ, соответственно (рис.11), тогда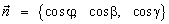 
. Причем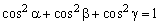 
. Величины cosα,
cosβ, cosγ называются направляющими косинусами вектора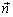
Глава 6. Скалярное произведение
Определение: Скалярным произведением двух векторов называется число,
Равное произведению длин этих векторов на косинус угла между ними. Если один из
