Скалярное произведение векторов 
и 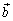 обозначается через
обозначается через 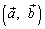
[или 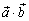 ; или
; или 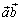
]. Если φ - угол между векторами 
и 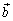 , то
, то 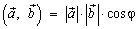
.
Скалярное произведение обладает следующими свойствами:
1. 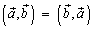 (коммутативность).
(коммутативность).
2. 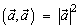 (скалярный квадрат вектора равен квадрату его длины).
(скалярный квадрат вектора равен квадрату его длины).
Скалярное произведение равно нулю тогда и только тогда, когда
Сомножители ортогональны или хотя бы один из них нулевой.
4. 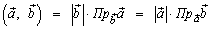 .
.
5. 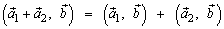 .
.
6. 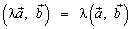 .
.
Теорема: В ортогональном базисе 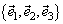 компоненты любого вектора
компоненты любого вектора  находятся по формулам:
находятся по формулам:
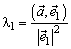 ;
; 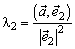 ;
; 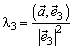 .
.
Действительно, пусть 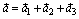 , причем
, причем
Каждое слагаемое коллинеарно соответствующему базисному вектору. Из теоремы
второго раздела следует, что 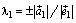 ,
,
 2015-04-12
2015-04-12 945
945








