Где выбирается знак плюс или минус в зависимости от того, одинаково или

противоположно направлены векторы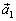

, и 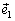. Но,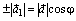

, где φ - угол между векторами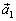

, и 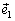. Итак,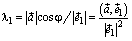

Аналогично вычисляются и остальные компоненты.

Скалярное произведение используется для решения следующих основных задач:

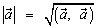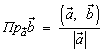1. ; 2. ; 3. .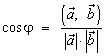

Пусть в некотором базисе 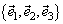заданы

векторы 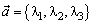и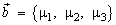

тогда, пользуясь свойствами скалярного произведения, можно записать:

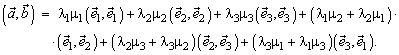
Величины 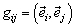называются метрическими коэффициентами данного базиса. Следовательно .

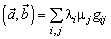Теорема: В ортонормированном базисе

;

;

;

.

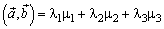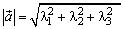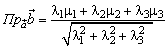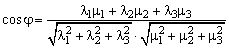Замечание: Все рассуждения этого раздела приведены для случая

Расположения векторов в пространстве. Случай расположения векторов на плоскости

Получается изъятием лишних компонент. Автор предлагает сделать вам это