Расстояние от точки до прямой, расстояние между скрещенными прямыми, угол между прямой и плоскостью

РАССТОЯНИЕ ОТ ТОЧКИ ДО ПРЯМОЙ

Расстояние d от данной точки 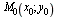до прямой l (под этим расстоянием понимается длина перпендикуляра, опущенного из точки 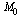на прямую l), заданной уравнением А х + B y + С = 0, определяется по формуле 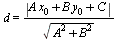(13)

Пример. Найдем расстояние от точки 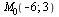до прямой 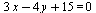. Согласно формуле (13) получим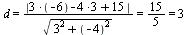

Угол между прямой и плоскостью- это угол, образованный прямой и ее проекцией на плоскость.

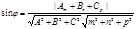
Угол между плоскостями.

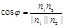, где n₁=(A₁ B₁ C₁); n₂=(A₂ B₂ C₂)

A₁A₂+B₁B₂+C₁C₂=0 |

A1/A2=B1/B2=C1/C2 УГОЛ МЕЖДУ ПРЯМОЙ И ПЛОСКОСТЬЮ

Углом между прямой и плоскостью будем называть угол, образованный прямой и её проекцией наплоскость. Пусть прямаяи плоскость заданы уравнениями

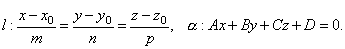
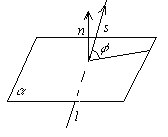Рассмотрим векторы 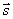и 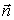. Если угол между ними острый, то он будет 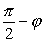, где φ – угол между прямой и плоскостью. Тогда .

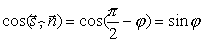Если угол между векторам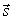и и 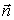тупой, то он равен 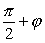. Следовательно 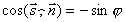. Поэтому в любом случае 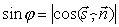. Вспомнив формулу вычисления косинуса угла между векторами, получим .

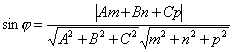Условие перпендикулярности прямой и плоскости. Прямая и плоскость перпендикулярны тогда и только тогда, когда направляющий вектор прямой 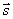и нормальный вектор 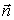плоскости коллинеарны, т.е. .

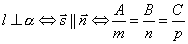Условие параллельности прямой и плоскости. Прямая и плоскость параллельны тогда и только тогда, когда векторы 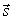и 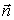перпендикулярны.