Примеры. Так как M1Î α, то уравнение плоскости будем искать в виде

1 2 3 4 5 6

Написать уравнение плоскости, проходящей через точку М ₁(2;-3;4) параллельно прямым 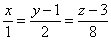и .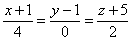

Так как M₁ Î α, то уравнение плоскости будем искать в виде

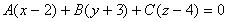Применяя условие параллельности прямой и плоскости, получим систему линейных уравнений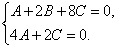

Отсюда

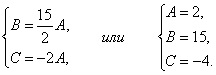
Итак, 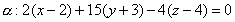или .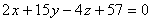

две прямые называются скрещивающимися, если они не лежат в одной плоскости.

Теорема.

Через каждую из скрещивающихся прямых проходит единственная плоскость, которой параллельна другая прямая.

Расстояние между скрещивающимися прямыми – это расстояние между одной из скрещивающихся прямых и параллельной ей плоскостью, проходящей через другую прямую.

В свою очередь расстояние между прямой и параллельной ей плоскостью есть расстояние от некоторой точки прямой до плоскости. Тогда справедлива следующая формулировка определения расстояния между скрещивающимися прямыми.

Определение.

Расстояние между скрещивающимися прямыми – это расстояние от некоторой точки одной из скрещивающихся прямых до плоскости, проходящей через другую прямую параллельно первой прямой.

Рассмотрим скрещивающиеся прямые a и b. Отметим на прямой a некоторую точку М₁, через прямую b проведем плоскость 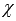, параллельную прямой a, и из точки М₁ опустим перпендикуляр М₁H₁ на плоскость 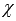. Длина перпендикуляра M₁H₁ есть расстояние между скрещивающимися прямыми a и b.