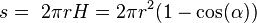Площадь сегмента сферы

, где H — высота сегмента, а 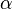— зенитный угол

[править]Сфера в трёхмерном пространстве

Уравнение

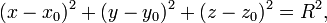
где 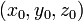— координаты центра сферы, 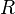— её радиус.

Параметрическое уравнение сферы с центром в точке :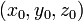

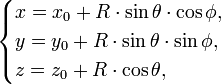
где 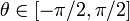и

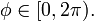
[править]Геометрия на сфере

Основная статья: Сферическая геометрия

Окружность, лежащая на сфере, центр которой совпадает с центром сферы, называется большим кругом (большой окружностью) сферы. Большие круги являются геодезическими линиями на сфере; любые два из них пересекаются в двух точках.

[править]Расстояние между двумя точками на сфере

Если даны сферические координаты двух точек, то расстояние между ними можно найти так:

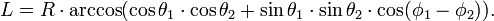
Однако, если угол 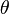задан не между осью Z и вектором на точку сферы, а между этим вектором и плоскостью XY (как это принято в земных координатах, заданных широтой и долготой), то формула будет такая:

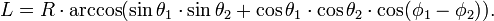
В этом случае 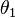и 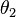называются широтами, а 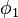и 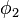долготами.

[править] n -мерная сфера

Основная статья: Гиперсфера

В общем случае уравнение (n -1)-мерной сферы (в n -мерном евклидовом пространстве) имеет вид:

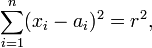
где 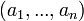— центр сферы, а — радиус.

Пересечением двух n -мерных сфер является n-1 -мерная сфера, лежащая на радикальной гиперплоскости этих сфер.

В n -мерном пространстве могут попарно касаться друг друга (в разных точках) не более n+1 сфер.

n -мерная инверсия переводит n-1 -мерную сферу в n-1 -мерную сферу или гиперплоскость.