Обозначения:
En – прямая при n = 1, плоскость при n = 2, пространство при n = 3 (с евклидовой геометрией)
Rn = 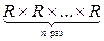
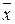 Î Rn – упорядоченный столбец n×1
Î Rn – упорядоченный столбец n×1
A (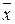 ) – координаты точки A в декартовой системе координат в En
) – координаты точки A в декартовой системе координат в En
Определение. Направленным отрезком в En будем назвать отрезок, у которого упорядочены концы (то есть один конец отрезка – первый, другой – второй)
Обозначение направленного отрезка:
|
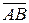 - направленный отрезок AB, у которого первый конец (начало) – точка A, второй конец (конец) – точка B.
- направленный отрезок AB, у которого первый конец (начало) – точка A, второй конец (конец) – точка B.
 Изображение направленного отрезка Изображение направленного отрезка 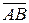 :
(точка A – начало, точка B - конец)
РИС. 19 :
(точка A – начало, точка B - конец)
РИС. 19
|
|
Вырожденный отрезок, у которого оба конца совпадают, будем понимать как направленный отрезок, начало и конец которого совпадают. Например, направленный отрезок 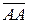
Определение. Длиной направленного отрезка называется расстояние между его началом и концом.
Обозначение: | 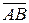 | - длина направленного отрезка
| - длина направленного отрезка 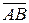 .
.
Пусть в En введена некоторая декартова система координат w.
Определение. Координаты направленного отрезка в системе координат w – это разность координат конца направленного отрезка и начала.
То есть если A(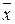 a), B(
a), B(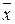 b), то координаты
b), то координаты  = (
= ( b-
b- 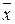 a).
a).
Замечание. Вычисление длины направленного отрезка в декартовой системе координат осуществляется по той же формуле, что и расстояние между точками. Если же координаты направленного отрезка уже известны, то квадрат его длины равен сумме квадратов координат этого отрезка.
Наблюдение. Все координаты направленного отрезка, у которого начало и конец совпадают, в любой декартовой системе координат равны нулю. Более того, если все координаты некоторого направленного отрезка в некоторой системе координат равны нулю, то начало и конец этого отрезка совпадают.
Пусть 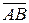 и
и 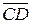 – направленные отрезки в En.
– направленные отрезки в En.
Определение. Будем говорить, что направленный отрезок 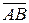 равен направленному отрезку
равен направленному отрезку 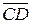 , если в системе координат w координаты отрезка
, если в системе координат w координаты отрезка 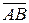 равны координатам отрезка
равны координатам отрезка 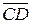 .
.
Обозначение равенства направленных отрезков: 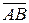 =
= 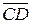 .
.
 2015-04-12
2015-04-12 425
425







