Существование.
Пусть  Î Vn, и координаты вектора
Î Vn, и координаты вектора  = (
= ( ), и пусть l Î R.
), и пусть l Î R.
Найдем вектор  = l
= l  .
.
Возьмем направленный отрезок 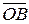 , где точка O – начало координат, точка B (l
, где точка O – начало координат, точка B (l  ).
).
Координаты этого направленного отрезка равны 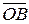 = (l
= (l  ).
).
Пусть вектор  такой, что
такой, что 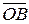 =
=  .
.
Тогда по определению  = l
= l  .
.
Единственность (в данной системе координат).
Пусть вектор 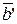 такой, что
такой, что 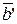 = l
= l  , тогда его координаты по определению
, тогда его координаты по определению 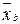 ’ = l
’ = l  , то есть
, то есть 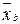 ’ =
’ = 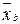 и
и 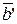 =
=  .
.
Лемма (Простейшие свойства умножения вектора на число (в данной системе координат)).
1) Если  = l
= l  , то |
, то |  | = | l | |
| = | l | |  | для любых векторов
| для любых векторов  ,
,  Î Vn и любого числа l Î R.
Î Vn и любого числа l Î R.
2) 0  = q для любого вектора
= q для любого вектора  Î Vn.
Î Vn.
3) lq = q для любого числа l Î R.
4) 1 ´  =
=  для любого вектора
для любого вектора  Î Vn.
Î Vn.
5) (l m)  = l (m
= l (m  ) = m (l
) = m (l  ) для любого вектора
) для любого вектора  Î Vn и любых чисел l, m Î R
Î Vn и любых чисел l, m Î R
 2015-04-12
2015-04-12 268
268








