Доказательство

1) Пусть = l и = , = .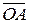

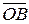Выразим координаты векторов и через координаты точек O,A и B:

координаты вектора : = -

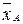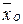
координаты вектора : = -

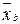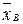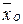
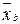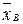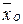Так как = l , то - = l (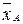 - 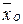), то есть 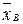= (1-l) 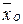+ l .

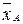Следовательно, точка B делит OA в отношении l.

2) Пусть точки O,A и B такие, что точка B делит OA в отношении l и = , = .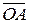

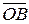Так как B делит OA в отношении l, то 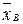= (1-l) 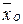+ l 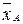, то есть

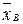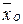- = l (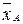 - 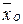), и координаты векторов и таковы, что 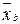= l .

Следовательно, = l .

Следствие. Если 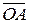= , 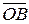= и = l (l Î R), то точки O,A,B лежат на одной прямой, более того при ≠ q, l > 0 лучи OA и OB совпадают,

при ≠ q, l < 0 лучи OA и OB являются дополнительными друг к другу.

Доказательство (непосредственно по определению «деления в отношении», см. § …)

Следствие. Умножение вектора на число не зависит от выбора системы координат.