Доказательство. 1. Пусть = l , и пусть координаты этих векторов =( )

1. Пусть = l , и пусть координаты этих векторов =(), = (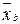). Тогда по определению 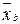= l .

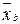Найдем длины этих векторов: | | = || ||, | | = || l || = | l | || || = | l | | |.

2. Пусть координаты вектора = (). Тогда координаты вектора 0 будут следующие: (0´ ) = q.

3. Так как все координаты нуль-вектора равны нулю, при умножении их на число l эти координаты останутся нулевыми, а значит, зададут нулевой вектор.

4. Координаты векторов и 1 ´ совпадают, так как координаты вектора при умножении число 1 не изменятся, следовательно, = 1 ´ .

5. Пусть координаты вектора = (). Найдем координаты векторов (l m) , l (m ) и m (l ): (l m) = (lm) , l (m ) = l(m )= (lm) , m (l ) = m (l ) = (l m) . Координаты данных векторов равны, следовательно и векторы равны друг другу.

Лемма. Пусть векторы , Î Vⁿ ( ≠ q) отложены от одной точки O так, что 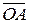= , 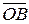= . Тогда для того чтобы = l (l Î R) необходимо и достаточно, чтобы точка B делила OA в отношении l.