Совместное исследование уравнений двух прямых

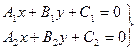
Каждое уравнение определяет прямую на плоскости. Совместное решение этих уравнений определяет общую точку этих прямых.

1). Пусть 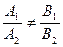. Определитель системы 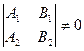, система имеет единственное решение.

Это значит, что прямые пересекаются в одной точке. Координаты точки пересечения находятся по формулам Крамера.

2). Пусть 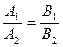. Тогда возможны два случая:

а) 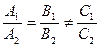=> общих точек нет, прямые параллельны;

б) 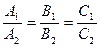=> уравнения равносильны, т.е. определяют одну и ту же прямую.

Два уравнения определяют одну прямую, если их коэффициенты пропорциональны.