Общее уравнение прямой

Теорема. В декартовой системе координат каждая прямая определяется уравнением первой степени и обратно, каждое уравнение первой степени определяет прямую.

Доказательство. Пусть существует прямая 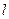. Если 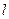не перпендикулярна оси Ох, то она определяется уравнением первой степени y = kx + b. Если прямая 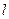перпендикулярна оси Ох, то для всех точек, принадлежащих прямой, выполняется равенство x = a, что также является уравнением первой степени.

Обратно. Пусть дано уравнение

Ax + By + C = 0. (7)

а). Если B ≠0, то можно записать 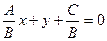или .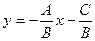

Обозначим 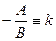и 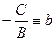. Тогда 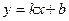– уравнение прямой.

б). Если В = 0, то А ≠ 0. 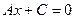=> x = .

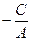Пусть 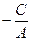≡ a => х = а – уравнение прямой, параллельной оси Oу.

Уравнение Ах + Ву + С = 0 называется общим уравнением прямой, поскольку определяет все виды прямых без исключения.