2015-04-12
551
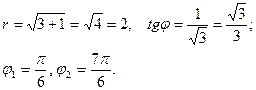
Равенства (4.25) примут вид: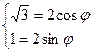 
Отсюда имеем:
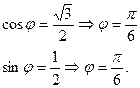
Таким образом, полярные координаты точки М равны: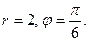 
Пример 3.. Дано полярное уравнение линии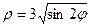 
. Построить эту линию по точкам. Найти ее декартово уравнение.
Решение. Выражение в правой части имеет смысл при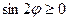 
, то есть 
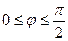и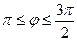 
. Учитывая периодичность функции (период Т= 
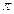) достаточно рассмотреть 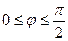. Составим таблицу значений функции, ограничиваясь точностью 0,01:
| 
| 
| 
| 
| 
| 
| |
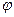
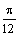
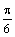
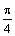
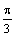
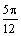
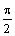
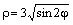
| 2,12 | 2,79 | 2,79 | 2,12 |
Проведем лучи, соответствующие выбранным значениям 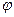, и на каждом из них отложим вычисленное значение 
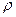. Полученные точки соединим плавной кривой (см. рис. ниже). Построенная линия называется лемнискатой Бернулли.
Чтобы перейти к декартовым координатам, запишем уравнение в виде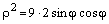 
и воспользуемся формулами (4.26, 4.28):
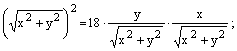
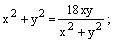
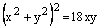
– уравнение линии в декартовой системе координат.
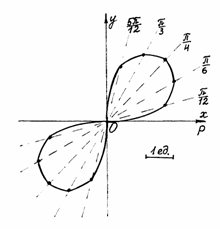
Рис.
Пример 4. Найти полярное уравнение окружности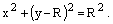 
Решение. Запишем уравнение в виде
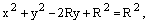или
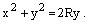
Воспользуемся формулами (4.25):
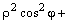
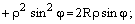
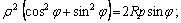
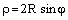– искомое уравнение.
|
|
|
