Уравнение кривых второго порядка с осями симметрии параллельными осям координат

Если в уравнении (4.12) кривой второго порядка 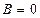, то каноническое уравнение можно получить с помощью параллельного переноса системы координат, при котором начало 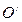новой системы 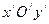помещается в точку 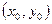, а «старые» и «новые» координаты связаны формулами:

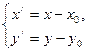(4.17)

Уравнение эллипса с центром 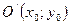имеет вид:

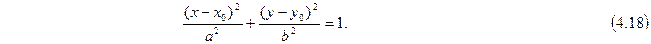Если ,

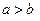то вершины эллипса 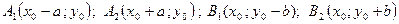, а фокусы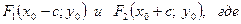

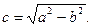
Если ,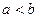

то вершины эллипса 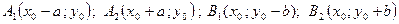, а фокусы

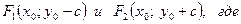
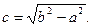
Уравнение гиперболы с центром 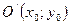имеет вид:

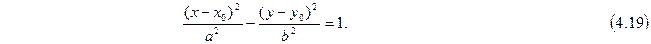
Вершины гиперболы 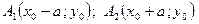, а фокусы

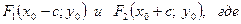
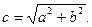
Уравнение сопряженной гиперболы с центром 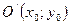имеет вид:

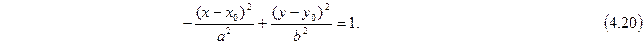Вершины гиперболы 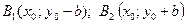а фокусы

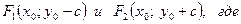
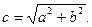
Уравнение параболы с вершиной 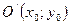с осью симметрии параллельной оси OX:

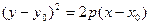(4.21)

или

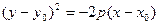(4.22)

Уравнение параболы с вершиной 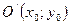с осью симметрии параллельной оси OY:

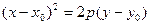(4.23)

или

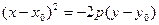(4.24)

Пример. Используя параллельный перенос системы координат привести уравнение кривой 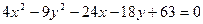к каноническому виду и построить кривую.

Решение. Преобразуем уравнение линии, группируя члены с 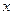и члены с 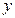, и вынося за скобки коэффициенты при квадратах:

,

;

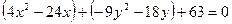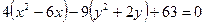выделим в скобках полные квадраты:

,

,

,

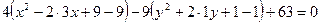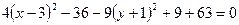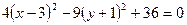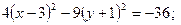
разделим обе части уравнения на (-36):

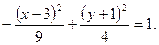
Получили уравнение сопряженной гиперболы (4.20) с центром в точке .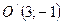

Выполним параллельный перенос

,

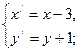
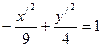получили каноническое уравнение гиперболы в систем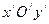е , где 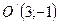- новое начало.