Для задания прямой в пространстве одного уравнения недостаточно. Это объясняется тем, что всякое уравнение 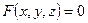 с тремя переменными
с тремя переменными 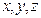 задает в пространстве некоторую поверхность
задает в пространстве некоторую поверхность 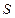 , а не линию.
, а не линию.
Рассмотрим различные виды уравнений прямой в пространстве.
1) Уравнения прямой, проходящей через точку 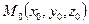 параллельно направляющему вектору
параллельно направляющему вектору 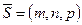
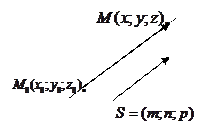 Рис. 5.4
Рис. 5.4
|
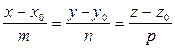 (5.9) (5.9)
|
Уравнения (5.9) называются каноническими уравнениями прямой.
Уравнения (5.9) получены из следующих соображений.
Если 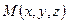 - произвольная точка прямой, то вектор
- произвольная точка прямой, то вектор 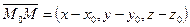 коллинеарен вектору
коллинеарен вектору 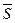 , а значит, их координаты пропорциональны, из чего и следуют уравнения (5.9).
, а значит, их координаты пропорциональны, из чего и следуют уравнения (5.9).
2) Уравнения прямой, проходящей через две точки 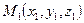 и
и 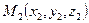 .
.
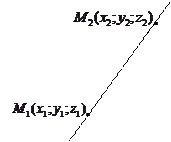 Рис. 5.5
Рис. 5.5
|
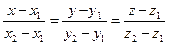 (5.10) (5.10)
|
Уравнения (5.10) также являются каноническими уравнениями прямой, так как числа, стоящие в знаменателях, есть координаты вектора 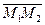 , являющегося направляющим для данной прямой.
, являющегося направляющим для данной прямой.
3) Параметрические уравнения прямой в пространстве:

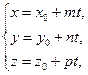 где
где 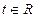 (5.11)
(5.11)
Уравнения (5.11) получаются из канонических уравнений (5.9), если все три отношения в них приравнять к некоторому параметру 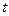 , а затем выразить
, а затем выразить 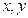 и
и 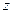 через
через 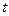 .
.
При этом 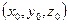 - координаты точки
- координаты точки 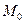 , через которую проходит прямая параллельно направляющему вектору
, через которую проходит прямая параллельно направляющему вектору 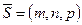 .
.
Замечание. Если какая–либо координата вектора 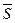 равна
равна 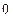 , то равен
, то равен 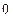 и знаменатель соответствующей дроби в уравнениях (5.9).
и знаменатель соответствующей дроби в уравнениях (5.9).
Не следует воспринимать такую дробь как деление на 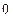 . Если, например,
. Если, например, 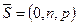 , то уравнения (5.9) примут вид:
, то уравнения (5.9) примут вид: 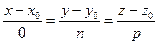 .
.
Перейдем к параметрическим уравнениям прямой. Получим
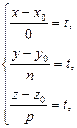 где
где 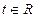 или
или 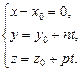
Первое уравнение 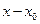 , означает, что прямая лежит на плоскости
, означает, что прямая лежит на плоскости 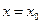 , перпендикулярной оси
, перпендикулярной оси 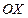 .
.
4) Общие уравнения прямой в пространстве
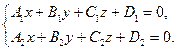 (5.12)
(5.12)
Уравнения (5.12) задают прямую, как линию пересечения двух плоскостей. Общие уравнения прямой могут быть преобразованы к каноническому или параметрическому виду.
5) Пусть даны две прямые, заданные каноническими уравнениями
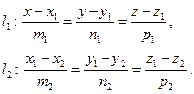
Угол 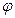 между прямыми
между прямыми 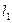 и
и 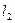 определяется, как угол между направляющими векторами данных прямых
определяется, как угол между направляющими векторами данных прямых 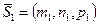 и
и 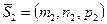 :
:
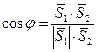 , или в координатной форме
, или в координатной форме
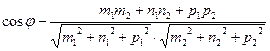 . (5.13)
. (5.13)
6) Условие параллельности двух прямых 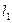 и
и 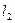 :
:
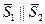 или
или 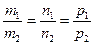 . (5.14)
. (5.14)
7) Условие перпендикулярности двух прямых 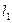 и
и 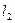 :
:
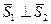 или
или 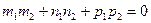 . (5.15)
. (5.15)
 2015-04-12
2015-04-12 447
447








