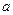Плоскость в пространстве можно задать различными способами; соответственно получим различные виды уравнений плоскости.
1) Уравнение плоскости, проходящей через точку 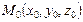 перпендикулярно нормальному вектору
перпендикулярно нормальному вектору 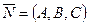 :
:
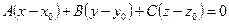 , (5.1)
, (5.1)
где 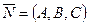 - нормаль.
- нормаль.
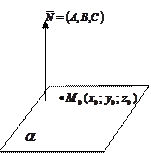
| Рис. 5.1 | Уравнение (5.1) получено из следующих соображений. Если 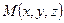 - произвольная точка плоскости - произвольная точка плоскости 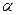 , то вектор , то вектор 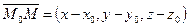 перпендикулярен нормали перпендикулярен нормали 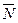 , т.е. , т.е. 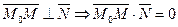 , откуда следует, что , откуда следует, что
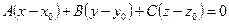 . .
|
2) Общее уравнение плоскости
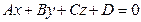 , (5.2)
, (5.2)
где коэффициенты 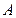 ,
, 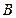 ,
, 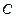 - координаты нормального вектора
- координаты нормального вектора 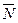 .
.
Уравнение (5.2) следует из уравнения (5.1), если в нем раскрыть скобки и число 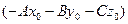 обозначить за
обозначить за 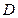 . Таким образом, плоскость задается уравнением первой степени относительно
. Таким образом, плоскость задается уравнением первой степени относительно 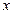 ,
, 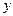 и
и 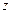 .
.
Верно и обратное утверждение: всякое уравнение первой степени вида (5.2) определяет в заданной прямоугольной системе координат плоскость.
3) Уравнение плоскости «в отрезках»
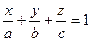 (5.3)
(5.3)
 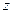
  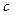
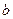
Рис.5.2 | где 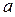 , , 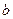 и и 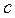 - величины направленных отрезков, отсекаемых плоскостью - величины направленных отрезков, отсекаемых плоскостью 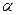 на координатных осях на координатных осях 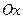 , , 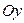 и и 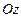 соответственно.
Уравнение (5.3) может быть получено из общего уравнения плоскости (5.2) переносом числа соответственно.
Уравнение (5.3) может быть получено из общего уравнения плоскости (5.2) переносом числа 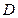 (если (если 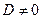 ) в правую часть равенства и делением уравнения на число ) в правую часть равенства и делением уравнения на число 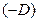 . .
|
4) Уравнение плоскости, проходящей через три точки 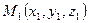 ,
, 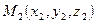 и
и 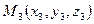 , не лежащие на одной прямой, может быть записано в виде:
, не лежащие на одной прямой, может быть записано в виде:
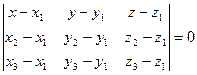 . (5.4)
. (5.4)
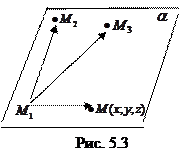
| Уравнение вида (5.4) получено из следующих соображений. Если 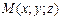 - произвольная точка плоскости - произвольная точка плоскости 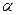 , то три вектора , то три вектора
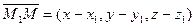 , , 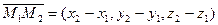 , ,
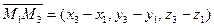
|
лежащие на плоскости 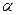 , компланарны, а следовательно, их смешанное произведение равно нулю, т.е.
, компланарны, а следовательно, их смешанное произведение равно нулю, т.е. 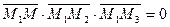 . Используя выражение смешанного произведения в координатной форме, получим уравнение (5.4).
. Используя выражение смешанного произведения в координатной форме, получим уравнение (5.4).
Если в уравнении (5.4) раскрыть определитель (лучше всего разложением по первой строке) и привести подобные члены, то получим уравнение вида (5.2).
5) Расстояние от точки 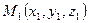 до плоскости
до плоскости 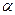 , заданной общим уравнением
, заданной общим уравнением 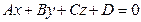 вычисляется по формуле:
вычисляется по формуле:
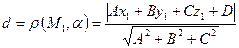 . (5.5)
. (5.5)
6) Угол между двумя плоскостями.
Пусть даны две плоскости:
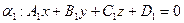 с нормалью
с нормалью 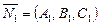 и
и
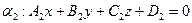 с нормалью
с нормалью 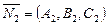 .
.
В качестве угла 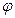 между плоскостями
между плоскостями 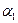 и
и 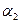 принимается угол между их нормалями:
принимается угол между их нормалями: 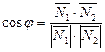 или в координатной форме
или в координатной форме
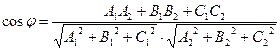 . (5.6)
. (5.6)
7) Условие параллельности двух плоскостей 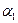 и
и 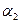 :
:
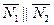 или в координатной форме
или в координатной форме
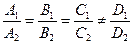 . (5.7)
. (5.7)
Если 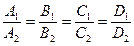 , то обе плоскости
, то обе плоскости 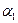 и
и 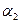 совпадают.
совпадают.
8) Условие перпендикулярности двух плоскостей 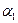 и
и 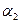 :
:
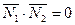 или в координатной форме
или в координатной форме
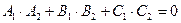 . (5.8)
. (5.8)
9) Неполные уравнения плоскости.
Общее уравнение плоскости 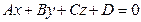 называется полным, если все его коэффициенты
называется полным, если все его коэффициенты 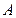 ,
, 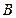 ,
, 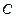 и
и 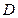 отличны от нуля. Если хотя бы один из коэффициентов равнее нулю, то уравнение (5.2) называется неполным.
отличны от нуля. Если хотя бы один из коэффициентов равнее нулю, то уравнение (5.2) называется неполным.
Рассмотрим различные виды неполных уравнений.
а) Если 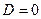 , то плоскость
, то плоскость 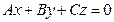 проходит через начало координат (поскольку координаты
проходит через начало координат (поскольку координаты 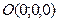 удовлетворяют этому уравнению);
удовлетворяют этому уравнению);
б) Если 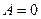 , то плоскость
, то плоскость 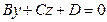 параллельна оси
параллельна оси 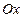 ;
;
в) Если 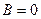 , то плоскость
, то плоскость 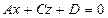 параллельна оси
параллельна оси 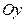 ;
;
г) Если 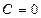 , то плоскость
, то плоскость 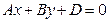 параллельна оси
параллельна оси 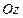 .
.
Признак параллельности плоскости координатной оси:
- если в уравнении нет переменной 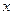 , то плоскость параллельна оси
, то плоскость параллельна оси 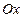 ;
;
- если в уравнении нет переменной 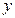 , то плоскость параллельна оси
, то плоскость параллельна оси 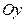 ;
;
- если в уравнении нет переменной 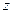 , то плоскость параллельна оси
, то плоскость параллельна оси 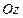 ,
,
т.е. плоскость параллельна той координатной оси, наименование которой отсутствует в уравнении плоскости.
д) Если 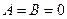 , то плоскость
, то плоскость 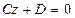 параллельна координатной плоскости
параллельна координатной плоскости 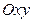 (так как эта плоскость одновременно параллельна оси
(так как эта плоскость одновременно параллельна оси 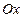 и оси
и оси 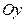 );
);
е) Если 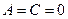 , то плоскость
, то плоскость 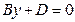 параллельна координатной плоскости
параллельна координатной плоскости 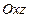 (так как эта плоскость одновременно параллельна оси
(так как эта плоскость одновременно параллельна оси 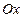 и оси
и оси 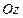 );
);
ж) Если 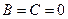 , то плоскость
, то плоскость 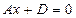 параллельна координатной плоскости
параллельна координатной плоскости 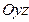 (так как эта плоскость одновременно параллельна оси
(так как эта плоскость одновременно параллельна оси 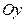 и оси
и оси 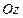 );
);
з) Если 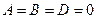 , то уравнение
, то уравнение 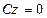
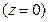 задает координатную плоскость
задает координатную плоскость 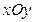 (так как плоскость параллельна плоскости
(так как плоскость параллельна плоскости 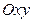 и проходит через начало координат);
и проходит через начало координат);
и) Если 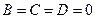 , то уравнение
, то уравнение 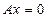
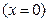 задает координатную плоскость
задает координатную плоскость 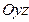 (так как плоскость параллельна плоскости
(так как плоскость параллельна плоскости 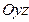 и проходит через начало координат);
и проходит через начало координат);
к) Если 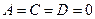 , то уравнение
, то уравнение 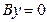
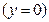 задает координатную плоскость
задает координатную плоскость 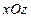 (так как плоскость параллельна плоскости
(так как плоскость параллельна плоскости 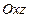 и проходит через начало координат).
и проходит через начало координат).
 2015-04-12
2015-04-12 549
549