Пример 1. Даны точки 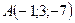 ,
, 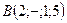 ,
, 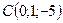 . Найти
. Найти 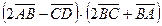 .
.
Решение. Определим координаты векторов, входящих в искомое скалярное произведение.
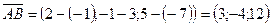 ,
,
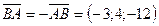 ,
,
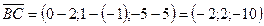 ,
,
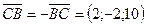 ,
,
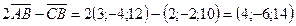 ,
,
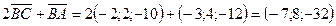 .
.
А теперь по формуле (3.23) найдем
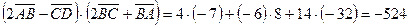 .
.
Пример 2. Найти 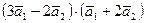 , если
, если 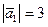 ,
, 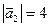 ,
, 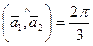 .
.
Решение. Для нахождения скалярного произведения воспользуемся его свойствами. По распределительному закону
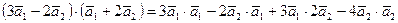 .
.
Упростим равенство с учетом 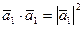 ,
, 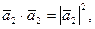
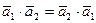 .
.
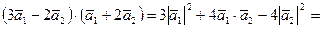
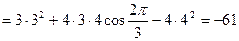 .
.
Пример 3. Найти угол между векторами 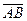 и
и 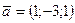 , если
, если 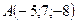 и
и 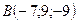 .
.
Решение. Обозначим вектором 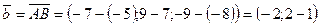 .
.
Найдем длины векторов 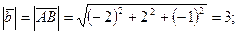
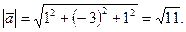 Определим скалярное произведение
Определим скалярное произведение 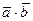 по формуле (3.23)
по формуле (3.23)
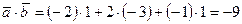 .
.
Теперь по формуле (3.24)
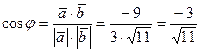 ,
,
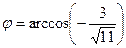 .
.
Пример 4. Даны векторы 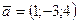 ,
, 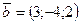 ,
, 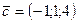 . Найти
. Найти 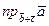 .
.
Решение. Используя формулу (3.26), запишем 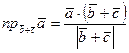 . Поскольку векторы заданы своими координатами, найдем по формуле (3.12) сумму векторов
. Поскольку векторы заданы своими координатами, найдем по формуле (3.12) сумму векторов
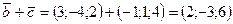
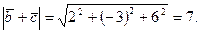 Определим величину скалярного произведения по формуле (3.23)
Определим величину скалярного произведения по формуле (3.23)
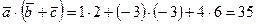 . Подставляем в формулу проекции, имеем
. Подставляем в формулу проекции, имеем
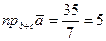 .
.
Пример 5. Найти координаты вектора 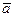 , перпендикулярного векторам
, перпендикулярного векторам 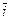 и
и 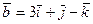 , если
, если 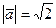 .
.
Решение. Обозначим неизвестные координаты вектора 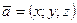 . Воспользуемся условием перпендикулярности векторов (3.22).
. Воспользуемся условием перпендикулярности векторов (3.22).
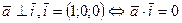 , откуда
, откуда 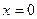 ;
;
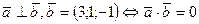 , значит
, значит 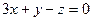 .
.
С учетом 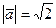 , т.е.
, т.е. 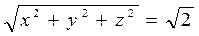 , получим систему
, получим систему
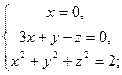
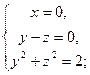
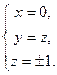
Условию задачи удовлетворяют два вектора 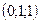 и
и 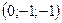 .
.
 2015-04-12
2015-04-12 444
444








